题目内容
2. 如图,反比例函数$y=\frac{k}{x}$(k≠0,k为常数)的图象与一次函数y=ax+b(a≠0,a、b为常数)的图象相交于A(-4,1)、B(2,m)两点.
如图,反比例函数$y=\frac{k}{x}$(k≠0,k为常数)的图象与一次函数y=ax+b(a≠0,a、b为常数)的图象相交于A(-4,1)、B(2,m)两点.(1)求k、m的值;
(2)求△AOB的面积;
(3)根据图象直接写出使不等式ax+b>$\frac{k}{x}$成立的x的取值范围.
分析 (1)将A坐标代入反比例解析式求出m的值,确定出反比例解析式,将B坐标代入反比例解析式求n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)设一次函数与x轴交于C点,求出C坐标,确定出OC的长,三角形AOB面积=三角形AOC面积+三角形BOC面积,求出即可.
(3)根据图象和交点坐标找出一次函数图象位于反比例函数图象上方时x的范围即可.
解答 解:(1)将A(-4,1)代入反比例解析式得:k=-4×1=-4,
则反比例解析式为y=-$\frac{4}{x}$;
将B(2,m)代入反比例解析式得:m=-2,即B(2,-2),
将A与B坐标代y=ax+b中,得:$\left\{\begin{array}{l}{-4a+b=1}\\{2a+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=-1}\end{array}\right.$.
则一次函数解析式为y=-$\frac{1}{2}$x-1;
(2)设一次函数与x轴交于点C,
对于一次函数y=-$\frac{1}{2}$x-1,令y=0,得到x=-2,即OC=2,
则S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×2=3.
(3)由图象得:不等式ax+b>$\frac{k}{x}$成立的x的取值范围为0<x<2或x<-4.
点评 此题考查了一次函数与反比例函数的交点问题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,利用了数形结合的思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
13.下列算式正确的是( )
| A. | $\sqrt{9}=3$ | B. | $\sqrt{4}=±2$ | C. | $\sqrt{0.9}=0.3$ | D. | $\sqrt{{{({-2})}^2}}=-2$ |
3.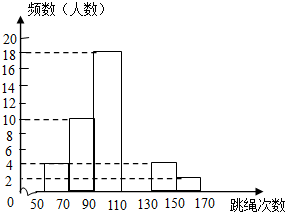 某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示),根据图表解答下列问题:
某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示),根据图表解答下列问题:
(1)a=10,b14.
(2)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则这50名男生中跳绳成绩为优秀的有多少人?优秀率为多少?
(3)若该校七年级入学时男生共有150人.请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
 某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示),根据图表解答下列问题:
某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示),根据图表解答下列问题:| 组别 | 次数x | 频数(人数) |
| 第1组 | 50≤x<70 | 2 |
| 第2组 | 70≤x<90 | a |
| 第3组 | 90≤x<110 | 18 |
| 第4组 | 110≤x<130 | b |
| 第5组 | 130≤x<150 | 4 |
| 第6组 | 150≤x<170 | 2 |
(2)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则这50名男生中跳绳成绩为优秀的有多少人?优秀率为多少?
(3)若该校七年级入学时男生共有150人.请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
7.下列各数中最小的是( )
| A. | 23 | B. | -32 | C. | (-3)2 | D. | (-2)3 |
 如图,在四边形ABCD中,∠BAD=90°,AB=AD,CB=CD,AE⊥BC垂足为点E,(BE<EC),AE=6$\sqrt{2}$,CD=5$\sqrt{2}$,连接DE,则DE的长为2$\sqrt{17}$或8.
如图,在四边形ABCD中,∠BAD=90°,AB=AD,CB=CD,AE⊥BC垂足为点E,(BE<EC),AE=6$\sqrt{2}$,CD=5$\sqrt{2}$,连接DE,则DE的长为2$\sqrt{17}$或8.