题目内容
已知:如图,AB、AC、ED分别切⊙O于点B、C、D,且AC⊥DE于E,BC的延长线交直线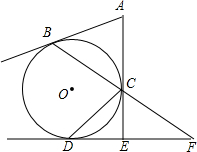 DE于点F.若BC=24,sin∠F=
DE于点F.若BC=24,sin∠F= .
.
(1)求EF的长;
(2)试判断直线AB与CD是否平行?若平行,给出证明;若不平行,说明理由.
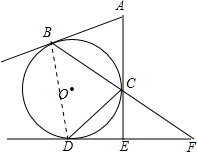 解:(1)在Rt△CEF中,∠CEF=90°,
解:(1)在Rt△CEF中,∠CEF=90°,由sin∠F=
 ,设CE=3x,CF=5x,
,设CE=3x,CF=5x,由勾股定理得EF=4x,
∵ED、EC分别切⊙O于点D、C,
∴ED=EC=3x,
由切割线定理得FD2=FC•FB,即(7x)2=5x•(5x+24),
∴x2-5x=0,
∴x1=5,x2=0(不合题意,舍去),
∴EF=4x=20;
(2)AB与CD不平行,
连接BD,
∵ED切⊙O于点D,
∴∠CBD=∠CDF,
又∵∠F=∠F,
∴△BDF∽△DCF,
∴
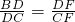 ,
,∵CF=5x=25,DF=7x=35,
在等腰直角△CDE中,可求得DC=15
 ,
,∴BD=21
 ,BC=24,
,BC=24,∴BD≠BC,
∴∠BDC≠∠BCD,
又∵AB切⊙O于点B,
∴∠ABC=∠BDC,
∴∠ABC≠∠BCD,
∴AB与CD不平行.
分析:(1)由sin∠F=
 ,设CE=3x,CF=5x,利用勾股定理可求EF,进而可求ED,再利用切割线定理可解出x,从而求出EF;(2)AB与CD不平行,连接BD,利用弦切角定理可知∠CDF=∠DBF,再加上一组公共角,那么易证△BDF∽△DCF,利用(1)中求出的x,可求出CF、DF、DC、BD的长,从而可以得出BD≠BC,即∠
,设CE=3x,CF=5x,利用勾股定理可求EF,进而可求ED,再利用切割线定理可解出x,从而求出EF;(2)AB与CD不平行,连接BD,利用弦切角定理可知∠CDF=∠DBF,再加上一组公共角,那么易证△BDF∽△DCF,利用(1)中求出的x,可求出CF、DF、DC、BD的长,从而可以得出BD≠BC,即∠BDC≠∠BCD,再结合弦切角定理可知∠ABC=∠BDC,从而得出∠ABC≠∠BCD,那么AB不平行于CD.
点评:本题利用了三角函数值、勾股定理、切割线定理、弦切角定理、相似三角形的判定和性质等知识.
(要证两直线不平行,即可证它们所夹的内错角不相等).

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( ) 已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.
已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.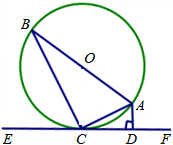 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
 29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD.
29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD. 已知:如图,AB=AC,DB=DC,求证:∠B=∠C.
已知:如图,AB=AC,DB=DC,求证:∠B=∠C.