题目内容
 如图,⊙M的圆心为M(-2,2),半径为2,直线AB过点A(0,-2),B(2,0),则⊙M关于y轴对称的⊙M′与直线AB的位置关系是
如图,⊙M的圆心为M(-2,2),半径为2,直线AB过点A(0,-2),B(2,0),则⊙M关于y轴对称的⊙M′与直线AB的位置关系是相交
相交
.分析:根据题意画出圆M关于y轴对称的圆M′,由图形可以直接得出结论:直线AB与⊙M′相交.
解答: 解:∵⊙M的圆心为M(-2,2),半径为2,
解:∵⊙M的圆心为M(-2,2),半径为2,
∴与⊙M关于y轴对称的⊙M′的圆心为M′(2,2),半径为2,如图所示.
根据图示知,直线AB与⊙M′相交;
故答案为:相交.
 解:∵⊙M的圆心为M(-2,2),半径为2,
解:∵⊙M的圆心为M(-2,2),半径为2,∴与⊙M关于y轴对称的⊙M′的圆心为M′(2,2),半径为2,如图所示.
根据图示知,直线AB与⊙M′相交;
故答案为:相交.
点评:此题考查了直线与圆的位置关系.此题难度不大,注意数形结合思想的应用,注意判断直线和圆的位置关系的方法:设⊙O的半径为r,圆心O到直线l的距离为d.①直线l和⊙O相交?d<r②直线l和⊙O相切?d=r③直线l和⊙O相离?d>r.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,⊙A的圆心为(4,0),半径为2,OP切⊙A于P点,则阴影部分的面积为( )
已知:如图,⊙A的圆心为(4,0),半径为2,OP切⊙A于P点,则阴影部分的面积为( )A、2
| ||||
B、2
| ||||
C、
| ||||
D、2
|
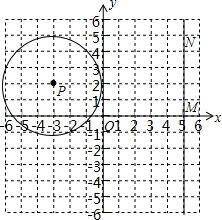 (2012•广州)如图,⊙P的圆心为P(-3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.
(2012•广州)如图,⊙P的圆心为P(-3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.
