题目内容

已知，在直角梯形ABCD中，AD∥BC，∠C=90°，AB = AD = 25，BC = 32．连接BD，AE⊥BD，垂足为点E．

①求证：△ABE∽△DBC；②求线段AE的长．

 


①证明：∵AB=AD=25，∴∠1 =∠2.∵AD∥BC，∴∠1=∠3.

∴∠2=∠3. ∵AE⊥BD，∴∠AEB=∠C=90°

∴△ABE∽△DBC.  ………5分

②解：∵AB=AD，又AE⊥BD，∴BE=DE.∴BD=2BE.

由△ABE∽△DBC，得

∵AB=AD=25，BC=32，∴.∴BE=20．

∴

=15． ………10分

练习册系列答案
相关题目
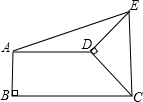已知：在直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=3，设∠BCD=a，以D为旋转中心，将腰精英家教网DC逆时针旋转90°至DE，连接AE、CE．
（1）当a=45°时，求△EAD的面积；
（2）当a=30°时，求△EAD的面积；
（3）当0°＜a＜90°时，猜想△EAD的面积与α大小有何关系？若有关，写出△EAD的面积S与a的关系式；若无关，请证明结论．
已知：在直角梯形COAB中，OC∥AB，以O为原点建立平面直角坐标系，A，B，C三点的坐标分别为A（8，0），B（8，10），C（0，4），点D为线段BC的中点，动点P从点O出发，以每秒1个单位的速度，沿折线OABD的路线移动，移动的时间为t秒．
（1）求直线BC的解析式；
（2）若动点P在线段OA上移动，当t为何值时，四边形OPDC的面积是梯形COAB面积的
27
；
（3）动点P从点O出发，沿折线OABD的路线移动过程中，设△OPD的面积为S，请写出S与t的精英家教网函数关系式，并指出自变量t的取值范围．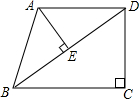
（2012•铁岭）已知：在直角梯形ABCD中，AD∥BC，∠C=90°，AB=AD=25，BC=32．连接BD，AE⊥BD垂足为E．
（1）求证：△ABE∽△DBC；
（2）求线段AE的长．
如图，已知：在直角梯形ABCD中，AB∥CD，AD⊥CD，AB=BC，又AE⊥BC于E
（1）求证：AD=AE；
（2）若∠B=60°，AD=3，求AC的长．
如图，已知：在直角梯形ABCD中，AB∥CD，AD⊥CD，AB=BC，又AE⊥BC于E．求证：AD=AE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网