题目内容
如图,A为⊙O外一点,AB切⊙O于点B,AO交⊙O于C,CD⊥OB于E,交⊙O于点D,连接OD.若AB=12,AC=8.
(1)求OD的长;
(2)求CD的长.
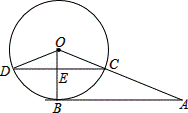
解:(1)设⊙O的半径为R,
∵AB切⊙O于点B,
∴OB⊥AB,
在Rt△ABO中,OB=R,AO=OC+AC=R+8,AB=12,
∵OB2+AB2=OA2,
∴R2+122=(R+8)2,解得R=5,
∴OD的长为5;
(2)∵CD⊥OB,
∴DE=CE,
而OB⊥AB,
∴CE∥AB,
∴△OEC∽△OBA,
∴ =
= ,即
,即 =
= ,
,
∴CE= ,
,
∴CD=2CE= .
.

练习册系列答案
相关题目
下列二次根式中,不能与 合并的是( )
合并的是( )
|
| A. |
| B. |
| C. |
| D. |
|
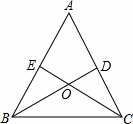
如图,在半径为6cm的⊙O中,点A是劣弧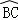 的中点,点D是优弧
的中点,点D是优弧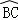 上一点,且∠D=30°,下列四个结论:
上一点,且∠D=30°,下列四个结论:
①OA⊥BC;②BC=6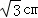 ;③sin∠AOB=
;③sin∠AOB=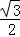 ;④四边形ABOC是菱形.
;④四边形ABOC是菱形.
其中正确结论的序号是( )

|
| A. | ①③ | B. | ①②③④ | C. | ②③④ | D. | ①③④ |




 )﹣1﹣|﹣5|+(
)﹣1﹣|﹣5|+( ﹣2)0
﹣2)0



 的解集为
的解集为