题目内容
2．若$\sqrt{3}$的整数部分为x，小数部分为y，则$\sqrt{3}$x-y的值是（ ）| A． | 1 | B． | $\sqrt{3}$ | C． | 3$\sqrt{3}$-3 | D． | 3 |
分析 先估算出$\sqrt{3}$的范围，求出x、y的值，再代入求出即可．
解答 解：∵1$＜\sqrt{3}＜2$，
∴x=1，y=$\sqrt{3}$-1，
∴$\sqrt{3}$x-y=$\sqrt{3}$×1-（$\sqrt{3}$-1）=1，
故选A．
点评 本题考查了估算无理数的大小，能估算出$\sqrt{3}$的范围是解此题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
13．下列各数中，是有理数是（ ）
| A． | $\frac{22}{7}$ | B． | π | C． | $\sqrt{2}$ | D． | $\sqrt{5}$ |
17．
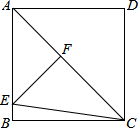如图，在正方形ABCD中，AC为对角线，点E在AB边上，EF⊥AC于点F，连接EC，AF=3，△EFC的周长为12，则EC的长为（ ）
如图，在正方形ABCD中，AC为对角线，点E在AB边上，EF⊥AC于点F，连接EC，AF=3，△EFC的周长为12，则EC的长为（ ）| A． | $\frac{7\sqrt{2}}{2}$ | B． | 3$\sqrt{2}$ | C． | 5 | D． | 6 |
7．
某工厂加工一批零件，为了提高工人工作积极性，工厂规定每名工人每次薪金如下：生产的零件不超过a件，则每件3元，超过a件，超过部分每件b元，如图是一名工人一天获得薪金y（元）与其生产的件数x（件）之间的函数关系式，则下列结论错误的是（ ）
某工厂加工一批零件，为了提高工人工作积极性，工厂规定每名工人每次薪金如下：生产的零件不超过a件，则每件3元，超过a件，超过部分每件b元，如图是一名工人一天获得薪金y（元）与其生产的件数x（件）之间的函数关系式，则下列结论错误的是（ ）| A． | a=20 | |
| B． | b=4 | |
| C． | 若工人甲一天获得薪金180元，则他共生产50件 | |
| D． | 若工人乙一天生产m（件），则他获得薪金4m元 |
14．下列运算结果是x+1的是（ ）
| A． | $\frac{{x}^{2}+1}{x+1}$ | B． | $\frac{1-{x}^{2}}{x+1}$ | C． | $\frac{x-1}{{x}^{2}-1}$ | D． | $\frac{{x}^{2}}{x-1}$$+\frac{1}{1-x}$ |
11．下列四个数中，比-4大的是（ ）
| A． | -5 | B． | -$\sqrt{20}$ | C． | -4.5 | D． | -2 |
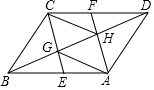如图，在?ABCD中，点E，F分别是AB，CD边上的两点，且BE=DF，连接CE，AF，分别交BD于点G，H，连接AG，CH．