题目内容
如图，P为等边三角形ABC内部一点，△ABP旋转后能与△CBP′重合．
（1）旋转中心是哪一点？旋转角是多少度？
（2）连接PP′，△BPP′是什么三角形？并说明你的理由．
解：（1）根据题意，AB与BC重合，所以旋转中心是点B，旋转角等于∠ABC=60°．
（2）△BPP′等边三角形．
∵旋转角为60°，即∠PBP′=60°，BP=BP′，
∴△BPP′等边三角形．
分析：（1）因为△ABC为等边三角形，所以AB=BC，∠ABC=60°．
△ABP旋转后能与△CBP′重合，显然是AB与BC重合，可判断是绕点B顺时钟旋转60°得到的．
（2）根据旋转角和对应边可判断△BPP′是等边三角形．
点评：结合图形，把握旋转的对应关系是解题的关键．
（2）△BPP′等边三角形．
∵旋转角为60°，即∠PBP′=60°，BP=BP′，
∴△BPP′等边三角形．
分析：（1）因为△ABC为等边三角形，所以AB=BC，∠ABC=60°．
△ABP旋转后能与△CBP′重合，显然是AB与BC重合，可判断是绕点B顺时钟旋转60°得到的．
（2）根据旋转角和对应边可判断△BPP′是等边三角形．
点评：结合图形，把握旋转的对应关系是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
3、如图，△ABC为等边三角形，∠ABC、∠ACB的平分线相交于点O，OE∥AB交BC于点E，OF∥AC交BC于点F，图中等腰三角形共有（ ）
如图，△ABC为等边三角形，点D，E，F分别在AB，BC，CA边上，且△DEF是等边三角形，求证：△ADF≌△CFE．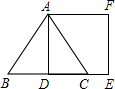
如图，△ABC为等边三角形，AD为BC边上的高，且AB=2，则正方形ADEF的面积为
如图，△ABC为等边三角形，D为△ABC内一点，△ABD逆时针旋转后到达△ACP位置，则∠APD=
如图①，△ABC为等边三角形，周长为p．D1，E1，F1分别是△ABC三边的中点，连接D1E1，E1F1，F1D1，可得△D1E1F1．