Question

（7分）已知：如图，在四边形ABCD中，BC<DC，∠BCD=60º，∠ADC=45º，CA平分∠BCD，，求四边形ABCD的面积.

Answer 1

S△ABCD=4.

解析试题分析：由于所求的四边形是一般的四边形，在求面积时，需要上，下底及高的值才可求出，本题不具有此条件，所以需做辅助线将四边形化为等面积的三角形以求之。.解：在CD上截取CF=CB，连结AF. 过点A作AE⊥CD于点E    1分；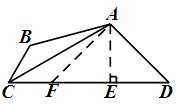

∵CA平分∠BCD ，∠BCD=60º，
∴，
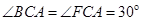在△ABC和△AFC中
∵ 
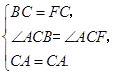
∴△ABC≌△AFC.         2分；
∴AF=AB ，
∵，
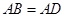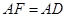∴.         3分；
在Rt△ADE中，，，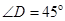
∴ sin，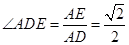
∴AE=ED="2" .      4分；
在Rt△AEC中，，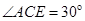
∴ tan，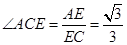
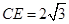∴.      5分；
∵AE⊥CD ，
∴FE=ED="2" .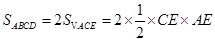
    6分；
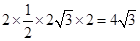=    7分.
注：另一种解法见下图，请酌情给分.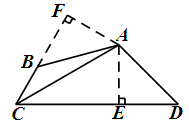

考点：四边形的面积，三角形的面积，三角形的全等判定，三角函数定义。
点评：本题求解有一定的难度，关键在画辅助线上，及把不规则的四边形变成可求的三角形，从而可求，解题时应用的知识面很多，需要对图形的认识能力很高，属于偏难题型。做法不唯一。