题目内容
7.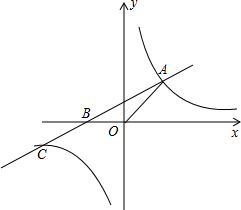 如图,直线y=x+2与x轴交于点B,与反比例函数y=(m+5)x2m+1的图象交于点A、C,其中点A在第一象限,点C在第三象限.
如图,直线y=x+2与x轴交于点B,与反比例函数y=(m+5)x2m+1的图象交于点A、C,其中点A在第一象限,点C在第三象限.(1)求此反比例函数的解析式及B点的坐标;
(2)若△AOB的面积为2,求A点的坐标;
(3)在(2)的条件下,在x轴上是否存在点P,使△AOP是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
分析 (1)根据反比例函数的定义得2m+1=-1,解方程得m=-1,于是得到反比例函数的解析式为$y=\frac{4}{x}$,把y=0代入y=x+2得x=-2,于是得到B点坐标为(-2,0);
(2)根据三角形面积公式得A点坐标为(2,2).
(3)分三种情况讨论即可求得.
解答 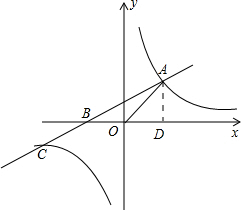 解:(1)由题意得:
解:(1)由题意得:
2m+1=-1,
m=-1.
故反比例函数的解析式为$y=\frac{4}{x}$;
由y=x+2可知B点的坐标为(-2,0)
(2)过点A作AD垂直x轴于D点
∵B点的坐标为(-2,0)
∴OB=2
∵三角形AOB的面积为2
∴$\frac{1}{2}$OB•AD=2,
∴AD=2,
把y=2代入y=$\frac{4}{x}$得x=2.
∴点A坐标是(2,2);
(3)存在;
∵点A坐标是(2,2),
∴OA=2$\sqrt{2}$,
当OP=OA时,P点的坐标为(-2$\sqrt{2}$,0)或(2$\sqrt{2}$,0);
当AP=OA时,P点的坐标为(4,0);
当AP=OP时,P点的坐标为(2,0).
综上,P点的坐标为(-2$\sqrt{2}$,0)或(2$\sqrt{2}$,0)或(4,0)或(2,0).
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目

 如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD且AC=12,BD=5,则梯形的高DE=$\frac{60}{13}$.
如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD且AC=12,BD=5,则梯形的高DE=$\frac{60}{13}$.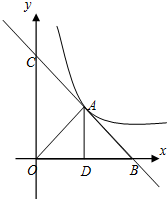 如图,一次函数的图象与反比例函数的图象在第一象限只有-个交点A,一次函数的图象与x轴、y轴分别交于B、C 两点,AD垂直平分OB,垂足为D,OA=$\sqrt{13}$,cos∠ABO=$\frac{{2\sqrt{13}}}{13}$.
如图,一次函数的图象与反比例函数的图象在第一象限只有-个交点A,一次函数的图象与x轴、y轴分别交于B、C 两点,AD垂直平分OB,垂足为D,OA=$\sqrt{13}$,cos∠ABO=$\frac{{2\sqrt{13}}}{13}$.