题目内容
 如图,直线MN和EF相交于点O,∠EON=45°,AO=2,∠AOE=15°,设点A关于EF的对称点是B,点B关于MN的对称点是C,则AC的距离为( )
如图,直线MN和EF相交于点O,∠EON=45°,AO=2,∠AOE=15°,设点A关于EF的对称点是B,点B关于MN的对称点是C,则AC的距离为( )分析:根据轴对称的性质得出∠AOB=∠BON=∠NOC=30°,进而利用勾股定理得出即可.
解答: 解:∵∠EON=45°,AO=2,∠AOE=15°,点A关于EF的对称点是B,点B关于MN的对称点是C,
解:∵∠EON=45°,AO=2,∠AOE=15°,点A关于EF的对称点是B,点B关于MN的对称点是C,
∴∠A0E=∠EOB,∠BON=∠NOC,AO=BO=CO=2,
∴∠AOB=∠BON=∠NOC=30°,
∴∠AOC=90°,
则AC的距离为:
=2
.
故选:D.
 解:∵∠EON=45°,AO=2,∠AOE=15°,点A关于EF的对称点是B,点B关于MN的对称点是C,
解:∵∠EON=45°,AO=2,∠AOE=15°,点A关于EF的对称点是B,点B关于MN的对称点是C,∴∠A0E=∠EOB,∠BON=∠NOC,AO=BO=CO=2,
∴∠AOB=∠BON=∠NOC=30°,
∴∠AOC=90°,
则AC的距离为:
| 22+22 |
| 2 |
故选:D.
点评:此题主要考查了轴对称图形的性质,根据已知得出∠A0E=∠EOB,∠BON=∠NOC,AO=BO=CO=2是解题关键.

练习册系列答案
相关题目
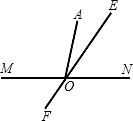 如图,直线MN和EF相交于点O,∠EON=60°,AO=2m,∠AOE=20°.设点A关于EF的对称点是B,点B关于MN的对称点是C,则A、C的距离为( )
如图,直线MN和EF相交于点O,∠EON=60°,AO=2m,∠AOE=20°.设点A关于EF的对称点是B,点B关于MN的对称点是C,则A、C的距离为( )
 C.
C.  D.
D. 


 m
m m
m m
m