Question

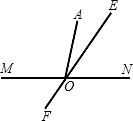如图，直线MN和EF相交于点O，∠EON=60°，AO=2m，∠AOE=20°．设点A关于EF的对称点是B，点B关于MN的对称点是C，则A、C的距离为（　　）

• A、

  3

  m
• B、2m
• C、2

  2

  m
• D、2

  3

  m

Answer 1

分析：根据轴对称的性质∠AOC=120°，所以∠ACO=30°，再作AD⊥OC构造出直角三角形，利用直角三角形30°角所对的直角边等于斜边的一半即可求解．

解答：解：根据题意OA=OC=2，
∵∠EON=60°，∠AOE=20°，
∴∠AOC=120°，
∴∠ACO=

1

2

×（180°-120°）=30°，
过点A作AD⊥CO于D，则OD=1，AD=

3

，
∴AC=2AD=2

3

m．
故选D．

点评：主要考查了轴对称的性质：（1）对应点所连的线段被对称轴垂直平分；（2）对应线段相等，对应角相等．