题目内容
如图,四边形ABDC中,∠D=∠ABD=90゜,点O为BD的中点,且OA平分 ∠BAC.

(1)求证:OC平分∠ACD;
(2)求证:AB+CD=AC.
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)过点O作OE⊥AC于E,根据角平分线上的点到角的两边的距离相等可得OB=OE,从而求出OE=OD,然后根据到角的两边距离相等的点在角的平分线上证明;
(2)利用“HL”证明△ABO和△AEO全等,根据全等三角形对应角相等可得∠AOB=∠AOE,同理求出∠COD=∠COE,然后求出∠AOC=90°,根据全等三角形对应边相等可得AB=AE,CD=CE,然后证明即可.
试题解析:(1)过点O作OE⊥AC于E,
∵∠ABD=90゜,OA平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
∴OC平分∠ACD;
(2)∵Rt△ABO≌Rt△AEO,
∴AB=AE,
同理可得CD=CE,
∵AC=AE+CE,
∴AB+CD=AC.
考点:角平分线的性质.

练习册系列答案
相关题目

 层.将图1倒置后与原图拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为
层.将图1倒置后与原图拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为 …
… .
.
 ,…,则最底层最左边这个圆圈中的数是 ;
,…,则最底层最左边这个圆圈中的数是 ; ,
,  ,
, ,…,求图4中所有圆圈中各数之和.
,…,求图4中所有圆圈中各数之和.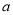 、
、 ,定义
,定义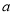 ⊙
⊙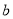
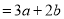 ,则[(x+y) ⊙(x-y)] ⊙3x化简后得( )
,则[(x+y) ⊙(x-y)] ⊙3x化简后得( )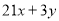 B.
B.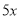 C.0 D.
C.0 D.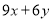
 这几个有理数中,负数的个数是( )
这几个有理数中,负数的个数是( )

 .
. 与
与 在此二次函数的图象上,则
在此二次函数的图象上,则
 (填 “>”、“=”或“<”);
(填 “>”、“=”或“<”); ,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
