题目内容
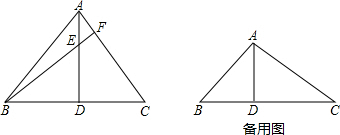
如图1,P是锐角△ABC所在平面上一点.如果∠APB=∠BPC=∠CPA=120°,则点P就叫做△ABC费马点.
(1)当△ABC是边长为4的等边三角形时,费马点P到BC边的距离为______.
(2)若点P是△ABC的费马点,∠ABC=60°,PA=2,PC=3,则PB的值为______.
(3)如图2,在锐角△ABC外侧作等边△ACB′,连接BB′.求证:BB′过△ABC的费马点P.

(1)解:延长AP,交BC于D,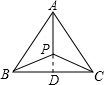
∵AB=AC=BC,∠APB=∠BPC=∠CPA=120°,
∴P为三角形的内心,
∴AD⊥BC,BD=CD=2,∠PBD=30°,
∴BP= =
= ,
,
∴AP=BP= ,
,
∵AD= =2
=2 ,
,
∴PD=AD-AP=2 -
- =
= ,
,
故答案为: .
.
(2)解:(1)∵∠PAB+∠PBA=180°-∠APB=60°,
∠PBC+∠PBA=∠ABC=60°,
∴∠PAB=∠PBC,
又∵∠APB=∠BPC=120°,
∴△ABP∽△BCP,
∴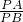 =
= ,
,
∴PB2=PA•PC,即PB= =
= ,
,
故答案为: .
.
(3)证明:在BB′上取点P,使∠BPC=120°
连接AP,再在PB′上截取PE=PC,连接CE.
∵∠BPC=120°,
∴∠EPC=60°,
∴△PCE为正三角形.
∴PC=CE,∠PCE=60°,∠CEB’=120°
∵△ACB′为正三角形,
∴AC=B′C,∠ACB′=60°
∴∠PCA+∠ACE=∠ACE+∠ECB′=60°,∠PCA=∠ECB′,
∴△ACP≌△B′CE,
∴∠APC=∠B′CE=120°,PA=EB′,
∴∠APB=∠APC=∠BPC=120°,
∴P为△ABC的费马点.
∴BB′过△ABC的费马点P.
分析:(1)延长AP,交BC于D,由等边三角形的性质可知AD⊥BC,BD=CD=2,∠BPC=30°,利用30°角的锐角三角函数值即可求出PD的长,即费马点P到BC边的距离;
(2)由题意可得△ABP∽△BCP,所以PB2=PA•PC,即PB= ;
;
(3)在BB'上取点P,使∠BPC=120°,连接AP,再在PB'上截取PE=PC,连接CE.由此可以证明△PCE为正三角形,再利用正三角形的性质得到PC=CE,∠PCE=60°,∠CEB'=120°,而△ACB'为正三角形,由此也可以得到AC=B'C,∠ACB'=60°,现在根据已知的条件可以证明△ACP≌△B'CE,然后利用全等三角形的性质即可证明题目的结论.
点评:此题考查了等腰三角形与等边三角形的性质及三角形内角和为180°等知识;此类已知三角形边之间的关系求角的度数的题,一般是利用等腰(等边)三角形的性质得出有关角的度数,进而求出所求角的度数.

∵AB=AC=BC,∠APB=∠BPC=∠CPA=120°,
∴P为三角形的内心,
∴AD⊥BC,BD=CD=2,∠PBD=30°,
∴BP=
 =
= ,
,∴AP=BP=
 ,
,∵AD=
 =2
=2 ,
,∴PD=AD-AP=2
 -
- =
= ,
,故答案为:
 .
.(2)解:(1)∵∠PAB+∠PBA=180°-∠APB=60°,
∠PBC+∠PBA=∠ABC=60°,
∴∠PAB=∠PBC,
又∵∠APB=∠BPC=120°,
∴△ABP∽△BCP,
∴
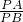 =
= ,
,∴PB2=PA•PC,即PB=
 =
= ,
,故答案为:
 .
.(3)证明:在BB′上取点P,使∠BPC=120°
连接AP,再在PB′上截取PE=PC,连接CE.
∵∠BPC=120°,
∴∠EPC=60°,
∴△PCE为正三角形.
∴PC=CE,∠PCE=60°,∠CEB’=120°
∵△ACB′为正三角形,
∴AC=B′C,∠ACB′=60°
∴∠PCA+∠ACE=∠ACE+∠ECB′=60°,∠PCA=∠ECB′,
∴△ACP≌△B′CE,
∴∠APC=∠B′CE=120°,PA=EB′,
∴∠APB=∠APC=∠BPC=120°,
∴P为△ABC的费马点.
∴BB′过△ABC的费马点P.
分析:(1)延长AP,交BC于D,由等边三角形的性质可知AD⊥BC,BD=CD=2,∠BPC=30°,利用30°角的锐角三角函数值即可求出PD的长,即费马点P到BC边的距离;
(2)由题意可得△ABP∽△BCP,所以PB2=PA•PC,即PB=
 ;
;(3)在BB'上取点P,使∠BPC=120°,连接AP,再在PB'上截取PE=PC,连接CE.由此可以证明△PCE为正三角形,再利用正三角形的性质得到PC=CE,∠PCE=60°,∠CEB'=120°,而△ACB'为正三角形,由此也可以得到AC=B'C,∠ACB'=60°,现在根据已知的条件可以证明△ACP≌△B'CE,然后利用全等三角形的性质即可证明题目的结论.
点评:此题考查了等腰三角形与等边三角形的性质及三角形内角和为180°等知识;此类已知三角形边之间的关系求角的度数的题,一般是利用等腰(等边)三角形的性质得出有关角的度数,进而求出所求角的度数.

练习册系列答案
相关题目
七年级我们曾学过“两点之间线段最短”的知识,常可利用它来解决两条线段和最小的相关问题,下面是大家非常熟悉的一道习题:
如图1,已知,A,B在直线l的同一侧,在l上求作一点,使得PA+PB最小.
|
|


我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.
有很多问题都可用类似的方法去思考解决.
探究:
1.如图3,正方形ABCD的边长为2,E为BC的中点, P是BD上一动点.连结EP,CP,则EP+CP的最小值是________;

运用:
2.如图4,平面直角坐标系中有三点A(6,4)、B(4,6)、C(0,2),在x轴上找一点D,使得四边形ABCD的周长最小,则点D的坐标应该是 ;
操作:
3.如图5,A是锐角MON内部任意一点,在∠MON的两边OM,ON上各求作一点B,C,组成△ABC,使△ABC周长最小.(不写作法,保留作图痕迹)