题目内容
【题目】二次函数y=![]() 的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B.C在函数图象上,四边形OBAC为菱形,且∠AOB=30
的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B.C在函数图象上,四边形OBAC为菱形,且∠AOB=30![]() ,则点C的坐标为( )
,则点C的坐标为( )

A. ![]() B.
B.  C.
C. 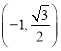 D.
D. ![]()
【答案】B
【解析】
连结BC交OA于D,如图,根据菱形的性质得BC⊥OA,∠OBD=60°,利用含30度的直角三角形三边的关系得OD=![]() BD,设BD=t,则OD=
BD,设BD=t,则OD=![]() t,B(t,
t,B(t,![]() t),利用二次函数图象上点的坐标特征得2
t),利用二次函数图象上点的坐标特征得2![]() t2=
t2=![]() t,得出BD=
t,得出BD=![]() ,OD=
,OD=![]() ,然后根据菱形的性质得出C点坐标.
,然后根据菱形的性质得出C点坐标.
解:连结BC交OA于D,如图,

∵四边形OBAC为菱形,
∴BC⊥OA,
∵∠AOB=30°,
∴∠OBD=60°,
∴OD=![]() BD,
BD,
设BD=t,则OD=![]() t,B(t,
t,B(t,![]() t)
t)
把B(t,![]() t)代入y=2
t)代入y=2![]() x2得2
x2得2![]() t2=
t2=![]() t,解得t1=0(舍去),t2=
t,解得t1=0(舍去),t2=![]() ,
,
∴BD=![]() ,OD=
,OD=![]() ,
,
故C点坐标为:(-![]() ,
,![]() ).
).
故选B.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目