题目内容
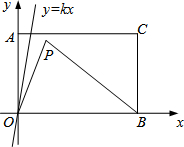
 如图,四边形OABC中,OA∥BC,点A在x轴上,点C在y轴上,OC=6,OA=OB=10,DE∥AB交AC于点P,且OP⊥DE,则点P的坐标是
如图,四边形OABC中,OA∥BC,点A在x轴上,点C在y轴上,OC=6,OA=OB=10,DE∥AB交AC于点P,且OP⊥DE,则点P的坐标是考点:一次函数综合题
专题:
分析:首先求出BC的长,即可得出B点坐标,延长OP,交AB于F,进而得出F点位置,进而求出直线PO解析式,进而得出直线AC的解析式,进而求出两函数交点坐标得出答案即可
解答:解:如图,

延长OP,交AB于F,
∵AB∥DE,OP⊥DE,
∴OP⊥AB,
又∵OA=OB,
∴点F是AB中点,
∵CB=
=8,
∴B点坐标(8,6),
又∵A(10,0),
∴AB的中点F点坐标为(9,3),
设PO的解析式为:y=ax,
∴9a=3,
解得:a=
,
∴OP的表达式为:y=
x,
∵A(10,0),C(0,6),
设AC的解析式为:y=kx+b,
,
解得:
∴AC的表达式为:y=-
x+6,
由
,
解得:
,
故点P的坐标为(
,
).
故答案为:(
,
).

延长OP,交AB于F,
∵AB∥DE,OP⊥DE,
∴OP⊥AB,
又∵OA=OB,
∴点F是AB中点,
∵CB=
| OB2-OC2 |
∴B点坐标(8,6),
又∵A(10,0),
∴AB的中点F点坐标为(9,3),
设PO的解析式为:y=ax,
∴9a=3,
解得:a=
| 1 |
| 3 |
∴OP的表达式为:y=
| 1 |
| 3 |
∵A(10,0),C(0,6),
设AC的解析式为:y=kx+b,
|
解得:
|
| 3 |
| 5 |
由
|
解得:
|
故点P的坐标为(
| 45 |
| 7 |
| 15 |
| 7 |
故答案为:(
| 45 |
| 7 |
| 15 |
| 7 |
点评:此题主要考查了一次函数的综合以及待定系数法求一次函数解析式以及函数交点求法等知识.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
已知OC平分∠AOB,则下列各式:
①∠AOB=2∠AOC;②∠BOC=∠AOB;③∠AOC=∠BOC;④∠AOB=∠BOC.
其中正确的是( )
①∠AOB=2∠AOC;②∠BOC=∠AOB;③∠AOC=∠BOC;④∠AOB=∠BOC.
其中正确的是( )
| A、①② | B、①③ | C、②④ | D、①②③ |
在下列实数中,最大的数是( )
| A、0 | ||
B、
| ||
| C、2 | ||
| D、-π |
 如图,在平面直角坐标系中,矩形AOBC的顶点A,B的坐标分别是A(0,4),B(
如图,在平面直角坐标系中,矩形AOBC的顶点A,B的坐标分别是A(0,4),B( 如图,在一次活动中,位于A处的甲班准备前往相距5km的B处与乙班会合,用方向和距离描述乙班相对于甲班位置是
如图,在一次活动中,位于A处的甲班准备前往相距5km的B处与乙班会合,用方向和距离描述乙班相对于甲班位置是 学校组织学生外出踏青,学生队伍从学校先步行出发,一段时间后王老师从学校骑车追赶学生,追上学生时接到电话要求王老师返回,因此王老师又立即按原速返回,当王老师回到学校时,学生还在继续前行,直到目的地.设王老师和学生队伍间的距离为y米,从王老师出发开始计时,设时间为x分钟,图中折线表示y与x的函数关系,则王老师比学生队伍的速度快
学校组织学生外出踏青,学生队伍从学校先步行出发,一段时间后王老师从学校骑车追赶学生,追上学生时接到电话要求王老师返回,因此王老师又立即按原速返回,当王老师回到学校时,学生还在继续前行,直到目的地.设王老师和学生队伍间的距离为y米,从王老师出发开始计时,设时间为x分钟,图中折线表示y与x的函数关系,则王老师比学生队伍的速度快 已知二次函数y=ax2+bx+c的图象如图所示,则下列7个代数式ab,ac,bc,b2-4ac,a+b+c,a-b+c,2a+b中,其值为正的式子的个数为
已知二次函数y=ax2+bx+c的图象如图所示,则下列7个代数式ab,ac,bc,b2-4ac,a+b+c,a-b+c,2a+b中,其值为正的式子的个数为