题目内容
已知a,b,c,为三角形三边,则a,b,c取下列各组数值组成直角三角形个数有
①a=7,b=24,c=25 ②a=12,b=18,c=22 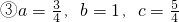 .
.
- A.1个
- B.2个
- C.3个
- D.0个
B
分析:根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形判定则可.
解答:①72+242=252,能组成直角三角形;
②122+182≠222,不能组成直角三角形;
③( )2+12=(
)2+12=( )2,能组成直角三角形.
)2,能组成直角三角形.
故选B.
点评:本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.
分析:根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形判定则可.
解答:①72+242=252,能组成直角三角形;
②122+182≠222,不能组成直角三角形;
③(
 )2+12=(
)2+12=( )2,能组成直角三角形.
)2,能组成直角三角形.故选B.
点评:本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成,一圆过A、D、E三点,求该圆半径的长.
已知多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成,一圆过A、D、E三点,求该圆半径的长.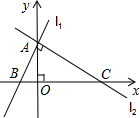 如图:已知,直线l1⊥l2,垂足为y轴上一点A,线段OA=2,OB=1.
如图:已知,直线l1⊥l2,垂足为y轴上一点A,线段OA=2,OB=1.