题目内容
如图(1),△ABC中,AB=AC,∠B=2∠A.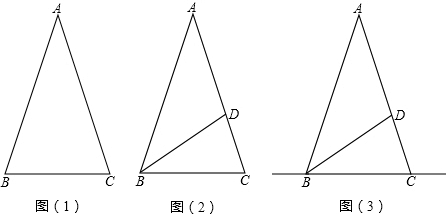
(1)求∠A和∠B的度数;
(2)如图(2),BD是△ABC中∠ABC的平分线:
①写出图中与BD相等的线段,并说明理由;
②直线BC上是否存在其它的点P,使△BDP为等腰三角形,如果存在,请在图(3)中画出满足条件的所有的点P,并直接写出相应的∠BDP的度数;如果不存在,请说明理由.
分析:(1)根据等腰三角形的性质和三角形的内角和定理进行计算;
(2)①结合(1)中的角的度数,又可以发现两个等腰三角形,即△ABD和△BCD,
②根据BD是底和BD是腰的时候,进行画图.根据等腰三角形的性质和三角形的内角和定理进行求解.
(2)①结合(1)中的角的度数,又可以发现两个等腰三角形,即△ABD和△BCD,
②根据BD是底和BD是腰的时候,进行画图.根据等腰三角形的性质和三角形的内角和定理进行求解.
解答:解:(1)∵AB=AC,∠B=2∠A
∴AB=AC,∠C=∠B=2∠A
又∵∠C+∠B+∠A=180°
∴5∠A=180°,∠A=36°
∴∠B=72°;
(2)①∵BD是△ABC中∠ABC的平分线
∴∠ABD=∠CBD=36°
∴∠BDC=72°
∴BD=AD=BC;
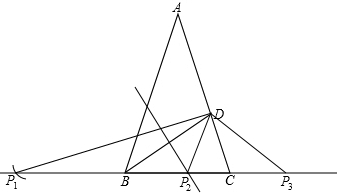
②当BD是腰时,以B为圆心,以BD为半径画弧,交直线BC于点P1(点C除外)
此时∠BDP=
∠DBC=18°.
以D为圆心,以BD为半径画弧,交直线BC于点P3(点C除外)
此时∠BDP=108°.
当BD是底时,则作BD的垂直平分线和BC的交点即是点P2的一个位置.
此时∠BDP=∠PBD=36°
∴AB=AC,∠C=∠B=2∠A
又∵∠C+∠B+∠A=180°
∴5∠A=180°,∠A=36°
∴∠B=72°;
(2)①∵BD是△ABC中∠ABC的平分线
∴∠ABD=∠CBD=36°
∴∠BDC=72°
∴BD=AD=BC;
②当BD是腰时,以B为圆心,以BD为半径画弧,交直线BC于点P1(点C除外)
此时∠BDP=
| 1 |
| 2 |
以D为圆心,以BD为半径画弧,交直线BC于点P3(点C除外)
此时∠BDP=108°.
当BD是底时,则作BD的垂直平分线和BC的交点即是点P2的一个位置.
此时∠BDP=∠PBD=36°

点评:本题主要考查了等腰三角形的判定和性质.找着角的关系利用内角和求角度是常用的方法,要熟练掌握.

练习册系列答案
相关题目
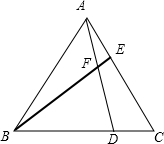 已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD.
已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD. 如图,在等腰直角△ABC中,∠ABC=90°,AB=BC,AD∥BC,E是AB的中点,BE=AD.
如图,在等腰直角△ABC中,∠ABC=90°,AB=BC,AD∥BC,E是AB的中点,BE=AD. 13、如图,△DEF是由△ABC平移得到的,若BC=6cm,E是BC的中点,则平移的距离是
13、如图,△DEF是由△ABC平移得到的,若BC=6cm,E是BC的中点,则平移的距离是 方作等边△CDE,连接BE.
方作等边△CDE,连接BE. 如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的
如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的