题目内容
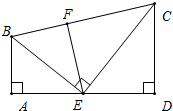 如图,AB⊥AD于点A,CD⊥AD于点D,∠ABC的平分线BE交AD于点E,且BE⊥CE于点E,EF⊥BC于点F,求证:AE=DE.
如图,AB⊥AD于点A,CD⊥AD于点D,∠ABC的平分线BE交AD于点E,且BE⊥CE于点E,EF⊥BC于点F,求证:AE=DE.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:由BE为角平分线,利用角平分线定义得到一对角相等,再由一对直角相等,BE为公共边,利用AAS得到三角形ABE与三角形FBE全等,利用全等三角形的对应边相等得到AE=FE,对应角相等得到∠AEB=∠FEB,利用等角的余角相等得到一对角相等,再由一对直角相等,CE=CE,利用AAS得到三角形EFC与三角形EDC全等,利用全等三角形对应边相等得到ED=FE,等量代换即可得证.
解答:证明:∵AB⊥AD,CD⊥AD,EF⊥BC,
∴∠A=∠EFB=90°,∠D=∠EFC=90°,
∵∠ABC的平分线BE交AD于点E,
∴∠FBE=∠ABE,
在△EAB和△EFB中,
,
∴△EAB≌△EFB(AAS),
∴AE=EF,∠AEB=∠FEB,
∵∠FEB+∠CEF=90°,∠AEB+∠CED=90°,
∴∠CEF=∠CED,
在△CEF和△CED中,
,
∴△CEF≌△CED(AAS),
∴EF=ED,
则AE=DE.
∴∠A=∠EFB=90°,∠D=∠EFC=90°,
∵∠ABC的平分线BE交AD于点E,
∴∠FBE=∠ABE,
在△EAB和△EFB中,
|
∴△EAB≌△EFB(AAS),
∴AE=EF,∠AEB=∠FEB,
∵∠FEB+∠CEF=90°,∠AEB+∠CED=90°,
∴∠CEF=∠CED,
在△CEF和△CED中,
|
∴△CEF≌△CED(AAS),
∴EF=ED,
则AE=DE.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若(a+
)2与|b+1|互为相反数,则的值为b-a=( )
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、1-
|
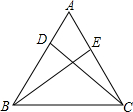 如图,若AB=AC,
如图,若AB=AC,