题目内容
仔细观察下列各式:2+2=2×2=22,22+22=2×22=23,23+23=2×23=24,…
(1)请你写出第4个等式;
(2)通过观察,相信你一定有所发现,请用等式表示你所发现的规律;
(3)利用上述信息,化简;22005-22004-22003-22002-22001-22000.
(1)请你写出第4个等式;
(2)通过观察,相信你一定有所发现,请用等式表示你所发现的规律;
(3)利用上述信息,化简;22005-22004-22003-22002-22001-22000.
考点:规律型:数字的变化类
专题:
分析:(1)两个相同乘方相加,等于一个乘方的2倍,由此直接写出答案即可;
(2)利用算式的规律得出第n个等式为2n+2n=2×2n=2n+1;
(3)利用乘方的意义,逐步两个两个计算得出答案即可.
(2)利用算式的规律得出第n个等式为2n+2n=2×2n=2n+1;
(3)利用乘方的意义,逐步两个两个计算得出答案即可.
解答:解:(1)第4个等式:24+24=2×24=25;
(2)第n个等式为2n+2n=2×2n=2n+1;
(3)22005-22004-22003-22002-22001-22000
=2×22004-22004-22003-22002-22001-22000.
=22004-22003-22002-22001-22000
=2×22003-22003-22002-22001-22000
=22003-22002-22001-22000
=2×22002-22002-22001-22000
=22002-22001-22000
=2×22001-22001-22000
=22001-22000
=2×22000-22000
=22000.
(2)第n个等式为2n+2n=2×2n=2n+1;
(3)22005-22004-22003-22002-22001-22000
=2×22004-22004-22003-22002-22001-22000.
=22004-22003-22002-22001-22000
=2×22003-22003-22002-22001-22000
=22003-22002-22001-22000
=2×22002-22002-22001-22000
=22002-22001-22000
=2×22001-22001-22000
=22001-22000
=2×22000-22000
=22000.
点评:此题考查数字的变化规律,发现等式之间的联系,找出规律,利用规律解决问题.

练习册系列答案
相关题目
 如图所示,在△ABC中,∠ABC=∠C=∠BDC,∠A=∠ABD,求∠A的度数.
如图所示,在△ABC中,∠ABC=∠C=∠BDC,∠A=∠ABD,求∠A的度数.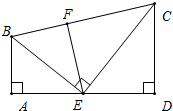 如图,AB⊥AD于点A,CD⊥AD于点D,∠ABC的平分线BE交AD于点E,且BE⊥CE于点E,EF⊥BC于点F,求证:AE=DE.
如图,AB⊥AD于点A,CD⊥AD于点D,∠ABC的平分线BE交AD于点E,且BE⊥CE于点E,EF⊥BC于点F,求证:AE=DE.