题目内容
【题目】如图,线段MN是周长为36cm的圆的直径(圆心为O),动点A从点M出发,以![]() 的速度沿顺时针方向在圆周上运动,经过点N时,其速度变为
的速度沿顺时针方向在圆周上运动,经过点N时,其速度变为![]() ,并以这个速度继续沿顺时针方向运动之点M后停止。在动点A运动的同时,动点B从点N出发,以
,并以这个速度继续沿顺时针方向运动之点M后停止。在动点A运动的同时,动点B从点N出发,以![]() 的速度沿逆时针方向在圆周上运动,绕一周后停止运动。设点A、点B运动时间为
的速度沿逆时针方向在圆周上运动,绕一周后停止运动。设点A、点B运动时间为![]() .
.
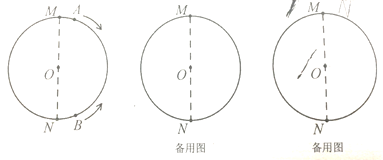
(1)连接OA、OB,当t=4时,![]() = °,在整个运动过程中,当
= °,在整个运动过程中,当![]() 时,点A运动的路程为 cm(第2空结果用含t的式子表示);
时,点A运动的路程为 cm(第2空结果用含t的式子表示);
(2)当A、B两点相遇时,求运动时间t;
(3)连接OA、OB,当![]() 时,请直接写出所有符合条件的运动时间t.
时,请直接写出所有符合条件的运动时间t.
【答案】(1)20;![]() ;(2)当A、B两点相遇时,t=
;(2)当A、B两点相遇时,t=![]() 或
或![]() ;(3)当
;(3)当![]() 时,t=3或
时,t=3或![]() 或12或
或12或![]()
【解析】
(1)根据圆O的周长,即可求出半圆![]() 的长,然后求出当t=4时,点A的运动路程
的长,然后求出当t=4时,点A的运动路程![]() 和点B的运动路程
和点B的运动路程![]() ,即可求出
,即可求出![]() ,然后求出
,然后求出![]() 占圆周长的分率乘360°即可求出
占圆周长的分率乘360°即可求出![]() ,画出
,画出![]() ,根据点A行驶的路程
,根据点A行驶的路程![]() =半圆
=半圆![]() +
+![]() 和速度即可求出结论;
和速度即可求出结论;
(2)根据第一次相遇和第二次相遇分类讨论,分别画出对应的图形,然后根据图形找出等量关系即可求出t的值;
(3)根据第一次相遇前![]() 、第一次相遇后
、第一次相遇后![]() 、第二次相遇前
、第二次相遇前![]() 、第二次相遇后
、第二次相遇后![]() ,分类讨论分别画出对应的图形,然后根据图形找出等量关系即可求出t的值.
,分类讨论分别画出对应的图形,然后根据图形找出等量关系即可求出t的值.
解:(1)∵圆O的周长为36cm
∴半圆![]() 的长为36÷2=18cm
的长为36÷2=18cm
当t=4时,根据题意可得![]() =3×4=12cm,
=3×4=12cm,![]() =2×4=8cm,如下图所示
=2×4=8cm,如下图所示

∴![]() =
=![]() +
+![]() -半圆
-半圆![]() =2cm
=2cm
∴∠AOB=![]()
点A到点N所需时间为18÷3=6s
当![]() 时,如下图所示
时,如下图所示

点A行驶的路程![]() =半圆
=半圆![]() +
+![]() =18+
=18+![]() =
=![]()
故答案为:20;![]() .
.
(2)当A、B两点第一次相遇时,如下图所示:
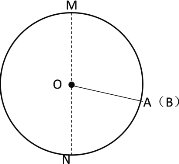
此时![]() +
+![]() =半圆
=半圆![]()
∴3t+2t=18
解得:t=![]() ;
;
当A、B两点第二次相遇时,如下图所示:

此时![]() +
+![]() -半圆
-半圆![]() =圆O的周长
=圆O的周长
即![]() +2t-18=36
+2t-18=36
解得:t=![]()
综上所述:当A、B两点相遇时,t=![]() 或
或![]() ;
;
(3)①当点A、B第一次相遇之前,∠AOB=30°时,如下图所示

此时![]() +
+![]() +
+![]() =半圆
=半圆![]()
即3t+![]() +2t=18
+2t=18
解得:t=3;
②当点A、B第一次相遇之后,∠AOB=30°时,如下图所示

此时![]() -
-![]() +
+![]() =半圆
=半圆![]()
即3t-![]() +2t=18
+2t=18
解得:t=![]() ;
;
③当点A、B第二次相遇之前,∠AOB=30°时,如下图所示
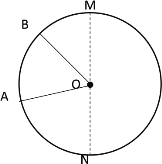
此时![]() +
+![]() -半圆
-半圆![]() +
+![]() =圆O的周长
=圆O的周长
即![]() +2t-18+
+2t-18+![]() =36
=36
解得:t=12;
④当点A、B第二次相遇之后,∠AOB=30°时,如下图所示
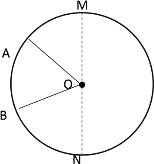
此时![]() +
+![]() -半圆
-半圆![]() -
-![]() =圆O的周长
=圆O的周长
即![]() +2t-18-
+2t-18-![]() =36
=36
解得:t=![]() ;
;
综上所述:当![]() 时,t=3或
时,t=3或![]() 或12或
或12或![]() .
.