题目内容
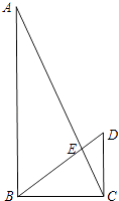
【题目】如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,AD=1,BC=2,求AB、CD的长.

【答案】AB=2![]() -2,CD=4-
-2,CD=4-![]() .
.
【解析】
此题为几何题,看题目只是一个四边形,要求两条未知边,那肯定要添辅助线.过点D作DH⊥BA延长线于H,作DM⊥BC于M.构建矩形HBMD.利用矩形的性质和解直角三角形来求AB、CD的长度.
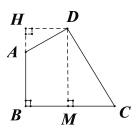
如图,过点D作DH⊥BA延长线于H,作DM⊥BC于点M.
∵∠B=90°,
∴四边形HBMD是矩形.
∴HD=BM,BH=MD,∠ABM=∠ADC=90°,
又∵∠C=60°,
∴∠ADH=∠MDC=30°,
∴在Rt△AHD中,AD=1,∠ADH=30°,则AH=![]() AD=
AD=![]() ,DH=
,DH=![]() .
.
∴MC=BC-BM=BC-DH=2-![]() =
=![]() .
.
∴在Rt△CMD中,CD=2MC=4-![]() ,DM=
,DM=![]() CD=
CD=![]() .
.
∴AB=BH-AH=DM-AH=![]() -
-![]() =
=![]()

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目