题目内容
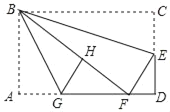
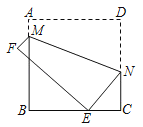
【题目】如图，将边长为8的正方形纸片ABCD折叠，使点D落在BC边的点E处，点A落在点F处，折痕为MN，若MN＝4
，则线段CN的长是____．
【答案】3
【解析】
过点M作MH⊥CD于点H．连接DE，结合题意可知MN垂直平分DE，先通过证明△MHN△DCE得出DE＝MN＝
，然后利用勾股定理求出CE的长，最后在Rt△ENC中利用勾股定理求出DN，最后进一步求出CN即可.
如图所示，过点M作MH⊥CD于点H．连接DE．
根据题意可知MN垂直平分DE，易证得：∠EDC＝∠NMH，MH＝AD，
∵四边形ABCD是正方形，
∴MH＝AD＝CD，
∵∠MHN＝∠C＝90°，
∴△MHN△DCE（ASA），
∴DE＝MN＝，
在Rt△DEC中，
，
设DN＝EN＝
，则CN＝
，
在Rt△ENC中，
，
∴
，
解得：
，
∴CN＝
，
故答案为：3．
练习册系列答案
相关题目
