Question

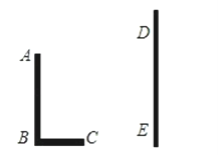
【题目】如图，在矩形纸片ABCD中，AB＝6，BC＝10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处，点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：①∠EBG＝45°；②S△ABG＝S△FGH；③△DEF∽△ABG；④AG+DF＝FG．其中正确的是_____．（把所有正确结论的序号都选上）

Answer 1

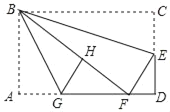
【答案】①②④．

【解析】

利用折叠性质得∠CBE=∠FBE，∠ABG=∠FBG，BF=BC=10，BH=BA=6，AG=GH，则可得到∠EBG=∠ABC，于是可对①进行判断；在Rt△ABF中利用勾股定理计算出AF=8，则DF=AD-AF=2，设AG=x，则GH=x，GF=8-x，HF=BF-BH=4，利用勾股定理得到x2+42=（8-x）2，解得x=3，所以AG=3，GF=5，于是可对②④进行判断；接着证明△ABF∽△DFE，利用相似比得到，而，所以，所以△DEF与△ABG不相似，于是可对③进行判断.

解：∵△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，

将△ABG沿BG折叠，点A恰落在线段BF上的点H处，

∴∠CBE＝∠FBE，∠ABG＝∠FBG，BF＝BC＝10，BH＝BA＝6，AG＝GH，

∴∠EBG＝∠EBF+∠FBG＝∠CBF+∠ABF＝∠ABC＝45°，所以①正确；

在Rt△ABF中，AF＝＝＝8，

∴DF＝AD﹣AF＝10﹣8＝2，

设AG＝x，则GH＝x，GF＝8﹣x，HF＝BF﹣BH＝10﹣6＝4，

在Rt△GFH中，

∵GH2+HF2＝GF2，

∴x2+42＝（8﹣x）2，解得x＝3，

∴GF＝5，

∴AG+DF＝FG＝5，所以④正确；

∵△BCE沿BE折叠，点C恰落在边AD上的点F处，

∴∠BFE＝∠C＝90°，

∴∠EFD+∠AFB＝90°，

而∠AFB+∠ABF＝90°，

∴∠ABF＝∠EFD，

∴△ABF∽△DFE，

∴＝，

∴＝＝＝，

而＝＝2，

∴≠，

∴△DEF与△ABG不相似；所以③错误．

∵S△ABG＝×6×3＝9，S△GHF＝×3×4＝6，

∴S△ABG＝S△FGH，所以②正确．

故答案是：①②④．