题目内容
7. 如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E,F,延长BD至G,使得DG=BD,连结EG,FG,若AE=DE,则$\frac{EG}{AB}$=$\frac{\sqrt{7}}{2}$.
如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E,F,延长BD至G,使得DG=BD,连结EG,FG,若AE=DE,则$\frac{EG}{AB}$=$\frac{\sqrt{7}}{2}$.
分析 连接AC、EF,根据菱形的对角线互相垂直平分可得AC⊥BD,根据线段垂直平分线上的点到线段两端点的距离相等可得AB=BD,然后判断出△ABD是等边三角形,再根据等边三角形的三个角都是60°求出∠ADB=60°,设EF与BD相交于点H,AB=4x,然后根据三角形的中位线平行于第三边并且等于第三边的一半求出EH,再求出DH,从而得到GH,利用勾股定理列式求出EG,最后求出比值即可.
解答  解:如图,连接AC、EF,
解:如图,连接AC、EF,
在菱形ABCD中,AC⊥BD,
∵BE⊥AD,AE=DE,
∴AB=BD,
又∵菱形的边AB=AD,
∴△ABD是等边三角形,
∴∠ADB=60°,
设EF与BD相交于点H,AB=4x,
∵AE=DE,
∴由菱形的对称性,CF=DF,
∴EF是△ACD的中位线,
∴DH=$\frac{1}{2}$DO=$\frac{1}{4}$BD=x,
在Rt△EDH中,EH=$\sqrt{3}$DH=$\sqrt{3}$x,
∵DG=BD,
∴GH=BD+DH=4x+x=5x,
在Rt△EGH中,由勾股定理得,EG=$\sqrt{E{H}^{2}+G{H}^{2}}$=$\sqrt{(\sqrt{3}x)^{2}+(5x)^{2}}$=2$\sqrt{7}$x,
所以,$\frac{EG}{AB}$=$\frac{2\sqrt{7}x}{4x}$=$\frac{\sqrt{7}}{2}$.
故答案为:$\frac{\sqrt{7}}{2}$.
点评 本题考查了菱形的性质,等边三角形的判定与性质,勾股定理,三角形的中位线平行于第三边并且等于第三边的一半,难点在于作辅助线构造出直角三角形以及三角形的中位线.

练习册系列答案
相关题目
2.下列四个数中,与-2的和为0的数是( )
| A. | -2 | B. | 2 | C. | 0 | D. | -$\frac{1}{2}$ |
15.下列各数中,比-2小的数是( )
| A. | -3 | B. | -1 | C. | 0 | D. | 2 |



 如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )
如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )
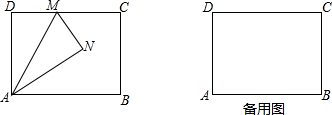
 如图,在?ABCD中,已知AD>AB.
如图,在?ABCD中,已知AD>AB.