题目内容
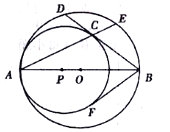
【题目】如图,![]() 为⊙
为⊙![]() 的直径,点
的直径,点![]() 是半径
是半径![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),
重合),![]() 为⊙
为⊙![]() 的半径,⊙
的半径,⊙![]() 的弦
的弦![]() 与⊙
与⊙![]() 相切于点
相切于点![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() .
.
(1)设![]() ,则
,则![]() 与
与![]() 之间的数量关系是什么?请说明理由.
之间的数量关系是什么?请说明理由.
(2)若![]() ,点
,点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
①当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]() 时,点
时,点![]() 是弦
是弦![]() 的中点.
的中点.
【答案】(1)![]() ,理由见解析;(2)①
,理由见解析;(2)①![]() ;②1
;②1
【解析】
(1)由切线的性质得90°,再利用三角形内角和推导两个角之间的关系;
(2)①由菱形得对角线互相垂直平分,构造出两个相似的三角形,再利用对应边成比例解方程即可;②由直径得垂直,由中点和垂直得垂直平分线,再利用圆的性质从而证得点O与点H重合即可.
证明:(1)2α-β=90°.
理由:连接PC.
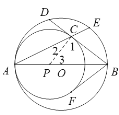
∵BD是⊙P的切线,
∴α+∠2=∠1=90°.
∴∠3+β=90°.
∵PA=PC,
∴∠A=∠2.
∵∠3是△APC的外角,
∴∠3=∠A+∠2=2∠2=2(90°-α).
∴2(90°-α)+ β= 90°.
整理,得2α-β=90°.
(2)①![]() ;
;
连接PC,
![]() ⊙
⊙![]() 的弦
的弦![]() 与⊙
与⊙![]() 相切于点
相切于点![]()
![]()
若四边形![]() 是菱形
是菱形
则![]() ,垂足为G,且
,垂足为G,且![]()
![]()
在△CGP和△BPC中,
![]() ,
,![]()
![]()
设![]() ,则
,则![]() ,
,![]()
![]()
![]() ,即
,即![]()
解得![]()
![]() 当
当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
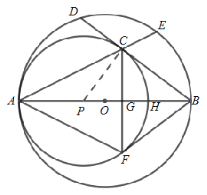
②1.
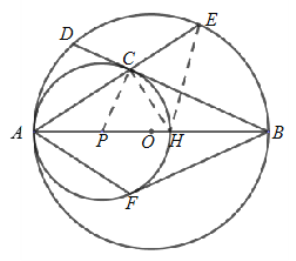
连接CH、EH
则![]()
即![]()
又![]() 点
点![]() 是弦
是弦![]() 的中点
的中点
![]()
故CH是弦AE的垂直平分线
又![]() 圆心O在弦AE的垂直平分线上
圆心O在弦AE的垂直平分线上
![]() 点O与点H重合
点O与点H重合
![]()
![]()

练习册系列答案
相关题目