题目内容
已知∠ABC=90°,AB=2,BC=3,AD∥BC,P为线段BD上的动点,点Q在射线AB上,且满足 (如图1所示).
(如图1所示).(1)当AD=2,且点Q与点B重合时(如图2所示),求线段PC的长;
(2)在图1中,连接AP.当AD=
 ,且点Q在线段AB上时,设点B、Q之间的距离为x,
,且点Q在线段AB上时,设点B、Q之间的距离为x, ,其中S△APQ表示△APQ的面积,S△PBC表示△PBC的面积,求y关于x的函数解析式,并写出函数定义域;
,其中S△APQ表示△APQ的面积,S△PBC表示△PBC的面积,求y关于x的函数解析式,并写出函数定义域;(3)当AD<AB,且点Q在线段AB的延长线上时(如图3所示),求∠QPC的大小.

【答案】分析:(1)当AD=2时,AD=AB,此时△ABD为等腰直角三角形,易证△BPC也是等腰直角三角形,BC长已知,则PC的长可求;
(2)易知点P到AB的距离与到BC的距离的比与BA、AD长度的比相等,即△APQ中AQ边上的高与△PBC中BC边上的高的比可求;AQ=2-x,BC=3,则△APQ与△BPC的面积可表示出来,利用其面积比为y,可得函数关系式;
(3)作PE⊥AB于E,PF⊥BC于F,由已知条件可证Rt△PCF∽Rt△PQE,则∠EPQ=∠FPC,利用角的和差关系可求得∠QPC=90°.
解答:解:(1)∵AD∥BC,∠ABC=90°,
∴∠A=∠ABC=90°.
当AD=2时,AD=AB,
∴∠D=∠ABD=45°,
∴∠PBC=∠D=45°.
∵ ,
,
∴PQ=PC,
∴∠C=∠PQC=45°,
∴∠BPC=90°.
∴PC=BC•sin45°=3× .
.
(2)如图,作PE⊥AB于E,PF⊥BC于F,
∵∠ABC=90°,
∴四边形EBFP是矩形.
∴PF=BE.
又∵∠BAD=90°,
∴PE∥AD,
∴Rt△BEP∽Rt△BAD.
∴ .
.
设BE=4k,则PE=3k,
∴PF=BE=4k.
∵BQ=x,
∴AQ=AB-BQ=2-x.
∴S△AQP= AQ•PE=
AQ•PE= (2-x)•3k,S△BPC=
(2-x)•3k,S△BPC= BC•PF=
BC•PF= ×3×4k=6k.
×3×4k=6k.
∵ ,
,
∴ ,
,
即y=- x+
x+ .
.
过D作BC的垂线DM,在直角△DCM中,DC= =
= =
= .
.
当P在D点时,x最大,则PC=DC= ,而
,而 ,得PQ=
,得PQ= ,利用勾股定理得到AQ=
,利用勾股定理得到AQ= ,所以此时BQ=
,所以此时BQ=
∴0≤x≤ .
.
(3)如图,作PE⊥AB于E,PF⊥BC于F,
∵∠ABC=90°,
∴四边形EBFP是矩形.
∴PF=BE,∠EPF=90°.
又∵∠A=90°,
∴PE∥AD.
∴Rt△BEP∽Rt△BAD.
∴ .
.
∴ .
.
又∵ ,
,
∴ .
.
∴Rt△PCF∽Rt△PQE,
∴∠EPQ=∠FPC.
∵∠EPQ+∠QPF=∠EPF=90°,
∴∠FPC+∠QPF=90°,
即∠QPC=90°.
点评:本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力.利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
(2)易知点P到AB的距离与到BC的距离的比与BA、AD长度的比相等,即△APQ中AQ边上的高与△PBC中BC边上的高的比可求;AQ=2-x,BC=3,则△APQ与△BPC的面积可表示出来,利用其面积比为y,可得函数关系式;
(3)作PE⊥AB于E,PF⊥BC于F,由已知条件可证Rt△PCF∽Rt△PQE,则∠EPQ=∠FPC,利用角的和差关系可求得∠QPC=90°.
解答:解:(1)∵AD∥BC,∠ABC=90°,
∴∠A=∠ABC=90°.
当AD=2时,AD=AB,
∴∠D=∠ABD=45°,
∴∠PBC=∠D=45°.
∵
 ,
,∴PQ=PC,
∴∠C=∠PQC=45°,
∴∠BPC=90°.
∴PC=BC•sin45°=3×
 .
.(2)如图,作PE⊥AB于E,PF⊥BC于F,
∵∠ABC=90°,
∴四边形EBFP是矩形.
∴PF=BE.

又∵∠BAD=90°,
∴PE∥AD,
∴Rt△BEP∽Rt△BAD.
∴
 .
.设BE=4k,则PE=3k,
∴PF=BE=4k.
∵BQ=x,
∴AQ=AB-BQ=2-x.
∴S△AQP=
 AQ•PE=
AQ•PE= (2-x)•3k,S△BPC=
(2-x)•3k,S△BPC= BC•PF=
BC•PF= ×3×4k=6k.
×3×4k=6k.∵
 ,
,∴
 ,
,即y=-
 x+
x+ .
.过D作BC的垂线DM,在直角△DCM中,DC=
 =
= =
= .
.当P在D点时,x最大,则PC=DC=
 ,而
,而 ,得PQ=
,得PQ= ,利用勾股定理得到AQ=
,利用勾股定理得到AQ= ,所以此时BQ=
,所以此时BQ=
∴0≤x≤
 .
.(3)如图,作PE⊥AB于E,PF⊥BC于F,

∵∠ABC=90°,
∴四边形EBFP是矩形.
∴PF=BE,∠EPF=90°.
又∵∠A=90°,
∴PE∥AD.
∴Rt△BEP∽Rt△BAD.
∴
 .
.∴
 .
.又∵
 ,
,∴
 .
.∴Rt△PCF∽Rt△PQE,
∴∠EPQ=∠FPC.
∵∠EPQ+∠QPF=∠EPF=90°,
∴∠FPC+∠QPF=90°,
即∠QPC=90°.
点评:本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力.利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.

练习册系列答案
相关题目
 26、如图,已知∠ABC=90°,∠1=∠2,∠DCA=∠CAB.
26、如图,已知∠ABC=90°,∠1=∠2,∠DCA=∠CAB.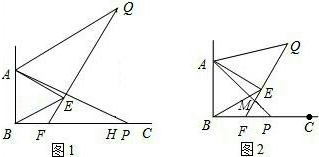
 (2012•惠山区一模)如图在三角形纸片ABC中,已知∠ABC=90°,AC=5,BC=4,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN,当点P在直线l上移动时,折痕的端点M、N也随之移动,若限定端点M、N分别在AB、BC边上移动,则线段AP长度的最大值与最小值的差为
(2012•惠山区一模)如图在三角形纸片ABC中,已知∠ABC=90°,AC=5,BC=4,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN,当点P在直线l上移动时,折痕的端点M、N也随之移动,若限定端点M、N分别在AB、BC边上移动,则线段AP长度的最大值与最小值的差为 如图,在Rt△ABC中,已知∠ABC=90°,以AB为直径作⊙O交AC于D,E为BC的中点,连接DE,求证:DE为⊙O的切线.
如图,在Rt△ABC中,已知∠ABC=90°,以AB为直径作⊙O交AC于D,E为BC的中点,连接DE,求证:DE为⊙O的切线.