题目内容
已知四边形ABCD内有一点E,满足EA=EB=EC=ED,且∠BCD=130°,那么∠BAD的度数为_____.
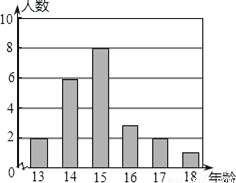
某校男子足球队队员的年龄分布为如图的条形图,则这些队员年龄的众数、中位数分别是_____。
现有60件某种产品,其中有3件次品,那么从中任意抽取1件产品恰好抽到次品的概率是_____。
查看答案如图,水平地面上有一面积为30πcm2的灰色扇形OAB,其中OA=6cm,且OA垂直于地面,将这个扇形向右滚动(无滑动)至点B刚好接触地面为止,则在这个滚动过程中,点O移动的距离是( )
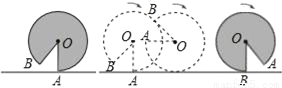
A. 10πcm B. 20πcm C. 24πcm D. 30πcm
查看答案若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是( )
A. k>﹣1 B. k>﹣1且k≠0 C. k<1 D. k<1且k≠0
查看答案在a2□4a□4的空格□中,任意填上“+”或“﹣”,在所有得到的代数式中,能构成完全平方式的概率是( )
A. 1 B. 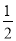 C.
C. 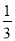 D.
D. 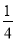
- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案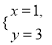 是二元一次方程
是二元一次方程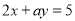 的一个解,则a的值为( )
的一个解,则a的值为( )
A. 1 B. 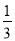 C. 3 D. -1
C. 3 D. -1
下列计算正确的是( )
A. 2a+3a=6a B. a2+a3=a5 C. a8÷a2=a6 D. (a3)4= a7
查看答案已知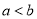 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A. 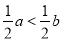 B.
B. 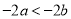 C.
C. 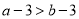 D.
D. 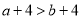
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.0000025米,把0.0000025用科学记数法表示为( )
A. 2.5×106 B. 0.25×10-5 C. 2.5×10-6 D. 25×10-7
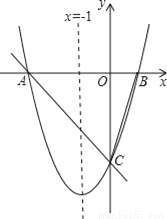
查看答案如图,对称轴为x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).
(1)求点B的坐标.
(2)已知a=1,C为抛物线与y轴的交点.
①若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标.
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
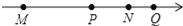
A. 点M B. 点N C. 点P D. 点Q
C 【解析】试题分析:∵点M,N表示的有理数互为相反数,∴原点的位置大约在O点, ∴绝对值最小的数的点是P点,故选C.下列说法,其中正确的个数为( )
①正数和负数统称为有理数;
②一个有理数不是整数就是分数;
③有最小的负数,没有最大的正数;
④符号相反的两个数互为相反数;
⑤﹣a一定在原点的左边.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案下列各题去括号所得结果正确的是( )
A. x2﹣(x﹣y+2z)=x2﹣x+y+2z B. x﹣(﹣2x+3y﹣1)=x+2x﹣3y+1
C. 3x﹣[5x﹣(x﹣1)]=3x﹣5x﹣x+1 D. (x﹣1)﹣(x2﹣2)=x﹣1﹣x2﹣2
查看答案若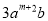 与
与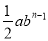 是同类项,则m+n=( )
是同类项,则m+n=( )
A. ﹣2 B. 2 C. 1 D. ﹣1
查看答案有四包真空包装的火腿肠,每包以标准质量450g为基准,超过的克数记作正数,不足的克数记作负数.下面的数据是记录结果,其中与标准质量最接近的是( )
A. +2 B. ﹣3 C. +4 D. ﹣1
查看答案如图,是一个正方形盒子的展开图,若要在展开后的其中的三个正方形A、B、C内分别填入适当的数,使得展开图折成正方体后相对的面上的两个数互为相反数,则填入正方形A、B、C内的三个数依次为( )
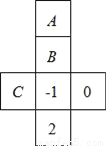
A. 1,﹣2,0 B. 0,﹣2,1 C. ﹣2,0,1 D. ﹣2,1,0
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之和能被3整除的概率.
(1)树状图见解析;(2). 【解析】试题分析:先根据题意画树状图,再根据所得结果计算两个数字之和能被3整除的概率. 试题解析:(1)树状图如下: (2)∵共6种情况,两个数字之和能被3整除的情况数有2种, ∴两个数字之和能被3整除的概率为, 即P(两个数字之和能被3整除)=.已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
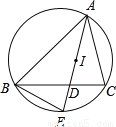
查看答案如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.求证:IE=BE.
市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
查看答案解方程:(1)2x2﹣5x+2=0;
(2)x+3﹣x(x+3)=0.
查看答案如图,AB是⊙O的直径,点C是半圆上的一个三等分点,点D是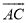 的中点,点P是直径AB上一点,若⊙O的半径为2,则PC+PD的最小值是_____.
的中点,点P是直径AB上一点,若⊙O的半径为2,则PC+PD的最小值是_____.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某种药品原来售价60元,连续两次降价后售价为48.6元,若每次下降的百分率相同,则这个百分率是_____.
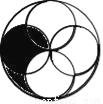
10﹪ 【解析】设每次下降的百分率为,根据题意可得: , 解得(不合题意,舍去), 所以每次下降的百分率为10%.如图,一个大圆和四个面积相等的小圆,已知大圆半径等于小圆直径,小圆半径为a厘米,那么阴影部分的面积为_____平方厘米.
若m是关于x的一元二次方程ax2+bx﹣5=0的一个根,则代数式am2+bm﹣7的值为_____。
查看答案一组数据的方差为S2,将该数据每一个数据,都乘以4,所得到的一组新数据的方差是_________。
查看答案若圆锥的底面半径为3,母线长为6,则圆锥的侧面积等于_____.
查看答案已知四边形ABCD内有一点E,满足EA=EB=EC=ED,且∠BCD=130°,那么∠BAD的度数为_____.

- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
在a2□4a□4的空格□中,任意填上“+”或“﹣”,在所有得到的代数式中,能构成完全平方式的概率是( )
A. 1 B. 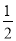 C.
C. 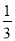 D.
D. 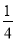
已知正六边形的边长为2,则它的内切圆的半径为( )
A. 1 B. 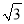 C. 2 D. 2
C. 2 D. 2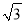
已知一组数据:16,15,16,14,17,16,15,则众数是( )
A. 17 B. 16 C. 15 D. 14
查看答案已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是( )
A. 相切 B. 相离 C. 相离或相切 D. 相切或相交
查看答案方程:x(x+1)=3(x+1)的解的情况是( )
A.x=﹣1 B.x=3 C.x1=﹣1,x2=3 D.以上答案都不对
查看答案已知:m,x,y满足:(1) ;(2)﹣2a2by+1与7b3a2是同类项.
;(2)﹣2a2by+1与7b3a2是同类项.
求代数式:2x2﹣6y2+m(xy﹣9y2)﹣(3x2﹣3xy+7y2)的值.
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
化简求值:(2x2y﹣4xy2)﹣(﹣3xy2+x2y),其中x=﹣1,y=2.
6. 【解析】试题分析:首先根据去括号的法则将括号去掉,然后再进行合并同类项计算,最后将x和y的值代入化简后的式子进行计算即可得出答案. 试题解析:【解析】 (2x2y﹣4xy2)﹣(﹣3xy2+x2y) =2x2y﹣4xy2+3xy2﹣x2y =x2y﹣xy2, 当x=﹣1,y=2时,原式=(﹣1)2×2﹣(﹣1)×22=1×2+1×4=2+4=6.如果规定符号“*”的意义是:a*b= ,试求2*(﹣4)的值.
,试求2*(﹣4)的值.
计算题
(1)﹣8﹣6+22﹣9.
(2)(﹣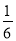 +
+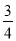 ﹣
﹣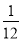 )×48.
)×48.
(3)|﹣0.75|+(﹣3)﹣(﹣0.25)+|﹣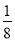 |+
|+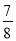 .
.
(4)﹣22+3×(﹣1)4﹣(﹣4)×5.
(5)(7m2n﹣5mn)﹣(4m2n﹣5mn)
(6)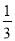 (9a﹣3)+2(a+1).
(9a﹣3)+2(a+1).
若|a|=3,|b|=2,且a>b,则a+b的值可能是:_____.
查看答案数轴上到点﹣3的距离是3个单位长度的点表示的数是_____.
查看答案已知单项式3amb2与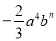 的和是单项式,那么m=_____,n=_____.
的和是单项式,那么m=_____,n=_____.
- 题型:解答题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
﹣2007的绝对值是( )
A. ﹣2007 B. ﹣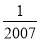 C.
C. 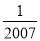 D. 2007
D. 2007
若规定收入为“+”,那么﹣50元表示( )
A.收入了50元
B.支出了50元
C.没有收入也没有支出
D.收入了100元
查看答案(1)阅读理【解析】
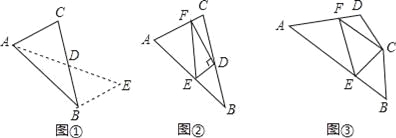
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
下面是某同学对多项式(x2﹣4x﹣3)(x2﹣4x+1)+4进行因式分解的过程.
【解析】
设x2﹣4x=y
原式=(y﹣3)(y+1)+4(第一步)
=y2﹣2y+1 (第二步)
=(y﹣1)2 (第三步)
=(x2﹣4x﹣1)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的 .
A.提取公因式法 B.平方差公式法 C.完全平方公式法
(2)请你模仿以上方法尝试对多项式(x2+2x)(x2+2x+2)+1进行因式分解.
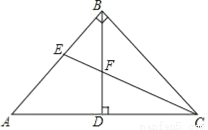
查看答案如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D;CE平分∠ACB,交AB于点E,交BD于点F.
(1)求证:△BEF是等腰三角形;
(2)求证:BD=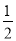 (BC+BF).
(BC+BF).
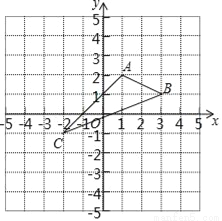
在平面直角坐标系中,A(1,2)、B(3,1)、C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出△ABC关于x轴对称△A2B2C2的各项点坐标A2 ,B2 ,C2 ;
(3)求△ABC的面积.
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
我国作家莫言获得诺贝尔文学奖之后,他的代表作品《蛙》的销售量就比获奖之前增长了180倍,达到2100000册,将2100000用科学记数法表示为( )
A. 0.21×108 B. 2.1×106 C. 2.1×107 D. 21×106
B 【解析】试题分析:科学计数法是指a×,且,n为原数的整数位数减一.两个数的和为正数,那么这两个数是( )
A. 正数 B. 负数
C. 至少有一个为正数 D. 一正一负
查看答案若|x|=4,|y|=7,且x+y>0,那么x﹣y的值是( )
A. 3或11 B. 3或﹣11 C. ﹣3或11 D. ﹣3或﹣11
查看答案数轴上一点A,一只蚂蚁从A出发爬了4个单位长度到了原点,则点A所表示的数是( )
A. 4 B. ﹣4 C. ±8 D. ±4
查看答案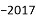
A. 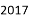
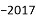
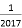 D.
D. 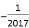
已知多项式A,B,计算A﹣B.某同学做此题时误将A﹣B看成了A+B,求得其结果为A+B=3m2﹣2m﹣5,若B=2m2﹣3m﹣2,请你帮助他求得正确答案.
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

