题目内容
（a-b）（a+b）=________
（a-b）（a2+ab+b2）=________
（a-b）________=a4-b4
（a-b）________=an-bn．
a2-b2 a3-b3 （a+b）（a2+b2） （an-1+an-2b+an-3b2+…+a2bn-3+abn-2+bn-1）
分析：根据平方差公式和立方差公式分别计算即可．
解答：∵由平方差公式得：（a-b）（a+b）=a2-b2；
由立方差公式得：（a-b）（a2+ab+b2）=a3-b3；
∴（a-b）（a+b）（a2+b2）=（a2-b2）（a2+b2）=a4-b4
（a-b）（an-1+an-2b+an-3b2+…+a2bn-3+abn-2+bn-1）=a（an-1+an-2b+an-3b2+…+a2bn-3+abn-2+bn-1）-b（an-1+an-2b+an-3b2+…+a2bn-3+abn-2+bn-1）=an-bn
故答案为：a2-b2 a3-b3 ）（a+b）（a2+b2），（an-1+an-2b+an-3b2+…+a2bn-3+abn-2+bn-1）．
点评：本题考查了平方差公式及立方差公式的知识，解题的关键是牢记公式并正确的理解公式的推导过程．
分析：根据平方差公式和立方差公式分别计算即可．
解答：∵由平方差公式得：（a-b）（a+b）=a2-b2；
由立方差公式得：（a-b）（a2+ab+b2）=a3-b3；
∴（a-b）（a+b）（a2+b2）=（a2-b2）（a2+b2）=a4-b4
（a-b）（an-1+an-2b+an-3b2+…+a2bn-3+abn-2+bn-1）=a（an-1+an-2b+an-3b2+…+a2bn-3+abn-2+bn-1）-b（an-1+an-2b+an-3b2+…+a2bn-3+abn-2+bn-1）=an-bn
故答案为：a2-b2 a3-b3 ）（a+b）（a2+b2），（an-1+an-2b+an-3b2+…+a2bn-3+abn-2+bn-1）．
点评：本题考查了平方差公式及立方差公式的知识，解题的关键是牢记公式并正确的理解公式的推导过程．
练习册系列答案
阅读快车系列答案
相关题目
的值等于0时，x的值为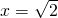
如图，在△ABC中，AC=AB，D为△ABC外一点，连接AD，交BC于E，若∠C=∠D，AE=6，DE=2，则AC的长是
能保证△ABC与△ACD相似的条件是