题目内容
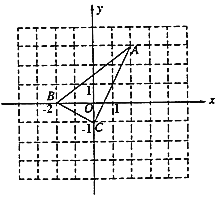
【题目】二次函数y=ax2+bx+c（a≠0）的部分图象如图③所示，图象过点（﹣1，0），对称轴为直线x=2，则下 列结论中正确的个数有（ ）
①4a+b=0；
②9a+3b+c＜0；
③若点A（﹣3，y1），点B（﹣
，y2），点C（5，y3）在该函数图象上，则y1＜y3＜y2；
④若方程a（x+1）（x﹣5）=﹣3的两根为x1和x2 ， 且x1＜x2 ， 则x1＜﹣1＜5＜x2 ．
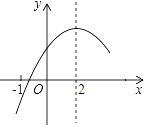
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】试题分析：对称轴为直线x=2，则
，则4a+b=0，则①正确；当x=3时函数值为正数，即
，则②错误；对于开口向下的函数，离对称轴越远，则函数值越小，则
，则③正确；根据函数图像可知：当y=-3时， 
，则④正确；故本题选C．
练习册系列答案
相关题目
【题目】为落实立德树人根本任务，培养德智体美劳全面发展的社会主义接班人，育才学校在设立学生奖学金时规定：每学期对学生的德智体美劳五个方面进行三次综合素质评价，分别是：假期综合素质评价、期中综合素质评价、期末综合素质评价，八年级（1）班的小明和八年级（2）班的小亮两位同学同时进入一等奖学金测评，他们的三次综合素质评价成绩如下表．
假期综合素质评价成绩 | 期中综合素质评价成绩 | 期末综合素质评价成绩 | |
小明 | 96 | 91 | 92 |
小亮 | 95 | 93 | 91 |
（1）如果从三次综合素质评价成绩稳定性的角度来看，谁可以得一等奖学金？请你通过计算回答；
（2）如果假期综合素质评价成绩、期中综合素质评价成绩、期末综合素质评价成绩按
的比例计入最终成绩，谁可以得一等奖学金？请你通过计算回答．
