题目内容
18．
如图，过正五边形ABCDE的顶点D作直线l∥AB，则∠1的度数是36°．
分析 根据正五边形的性质求出∠DCB=∠ABC=$\frac{1}{5}$×（5-2）×180°=108°，求出∠OCB=∠OBC=72°，根据三角形内角和定理求出∠O，根据平行线的性质得出∠1=∠O，代入求出即可．
解答 解：
延长DC、AB交于O，
∵五边形ABCDE是正五边形，
∴∠DCB=∠ABC=$\frac{1}{5}$×（5-2）×180°=108°，
∴∠OCB=∠OBC=180°-108°=72°，
∴∠O=180°-72°-72°=36°，
∵直线l∥AB，
∴∠1=∠O=36°，
故答案为：36°．
点评 本题考查了多边形和平行线的性质的应用，能正确作出辅助线是解此题的关键，注意：两直线平行，内错角相等．
练习册系列答案
相关题目
9．
某校对八年级300名学生就“分组合作学习”方式的支持程度进行了调查，随机抽取了若干名学生进行调查，并制作统计图，据此统计图估计该校八年级支持“分组合作学习”方式的学生（含非常喜欢和喜欢两种情况）约为（ ）
某校对八年级300名学生就“分组合作学习”方式的支持程度进行了调查，随机抽取了若干名学生进行调查，并制作统计图，据此统计图估计该校八年级支持“分组合作学习”方式的学生（含非常喜欢和喜欢两种情况）约为（ ）| A． | 180名 | B． | 210名 | C． | 240名 | D． | 270名 |
6．下列各数中，不是无理数的是（ ）
| A． | $\sqrt{5}$ | B． | -3.14 | C． | $\root{3}{36}$ | D． | $\frac{π}{3}$ |
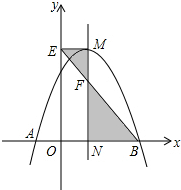如图，抛物线y=ax2+2x+c与x轴交于A，B两点，它的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连接BE交MN于点F，已知点A的坐标为（-1，0），B的坐标为（3，0）．
观察中国象棋的棋盘，其中“马”的位置可以用一个数对（3，5）来表示，则表示“兵”点位置的数对是（6，7）．