题目内容
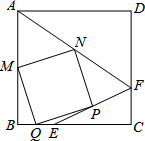 如图,在正方形ABCD中,E,F分别在BC,CD上,且BE=CF,M,N,P,Q分别是AB,AF,EF,BE的中点,判断四边形MNPQ的形状,并证明.
如图,在正方形ABCD中,E,F分别在BC,CD上,且BE=CF,M,N,P,Q分别是AB,AF,EF,BE的中点,判断四边形MNPQ的形状,并证明.考点:中点四边形
专题:
分析:首先证明△ABE≌△BCF,利用全等的性质证明AE=BF,AE⊥BF,即四边形ABEF的对角线互相垂直且相等,根据三角形中位线的性质可证明四边形MNPQ是正方形.
解答: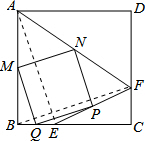 解:四边形MNPQ是正方形.理由如下:
解:四边形MNPQ是正方形.理由如下:
如图,连接AE、BF.
在△ABE和△BCF中,
,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
又∵∠BAE+∠BEA=90°,
∴∠BEA+∠CBF=90°,
∴AE⊥BF.
∵M,N分别是AB,AF的中点,
∵MN为△ABF的中位线,
∴MN=
BF,MN∥BF,
同理可证PQ=
BF,PQ∥BF,
即MN=PQ,MN∥PQ,四边形MNPQ为平行四边形,
易证NP=
AE=
BF=MN,
∴?PQGH菱形,
∵AE⊥BF,
∴NP⊥MN,菱形MNPQ为正方形.
 解:四边形MNPQ是正方形.理由如下:
解:四边形MNPQ是正方形.理由如下:如图,连接AE、BF.
在△ABE和△BCF中,
|
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
又∵∠BAE+∠BEA=90°,
∴∠BEA+∠CBF=90°,
∴AE⊥BF.
∵M,N分别是AB,AF的中点,
∵MN为△ABF的中位线,
∴MN=
| 1 |
| 2 |
同理可证PQ=
| 1 |
| 2 |
即MN=PQ,MN∥PQ,四边形MNPQ为平行四边形,
易证NP=
| 1 |
| 2 |
| 1 |
| 2 |
∴?PQGH菱形,
∵AE⊥BF,
∴NP⊥MN,菱形MNPQ为正方形.
点评:本题考查了中点四边形.关键是利用正方形的性质证明三角形全等,利用性质证明AE与BF的相等与垂直关系.

练习册系列答案
相关题目
计算:6
×
÷2
的结果是( )
| 7 |
| 1 |
| 3 |
| 21 |
| 3 |
| A、-4 | ||
B、-2
| ||
| C、40 | ||
| D、7 |
 某市出租车管理处公示的出租车运价如图:
某市出租车管理处公示的出租车运价如图: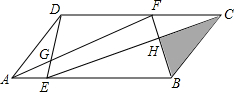 图中ABCD是平行四边形,面积是1,F为DC边上一点,E为AB上一点,连接AF,BF,DE,CE,AF交DE于G,EC交FB于H.已知,
图中ABCD是平行四边形,面积是1,F为DC边上一点,E为AB上一点,连接AF,BF,DE,CE,AF交DE于G,EC交FB于H.已知,
 (1)如图1,两个相同的正方形重叠摆放,若在图形中随机取点(不包括边线),则点取在阴影部分的概率是
(1)如图1,两个相同的正方形重叠摆放,若在图形中随机取点(不包括边线),则点取在阴影部分的概率是