题目内容
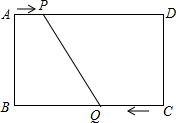 如图,在长方形ABCD中,AD=BC=12cm,AB=DC=8cm,动点P从点A出发沿AD向点D运动,速度是1cm/s,动点Q从点C出发沿CB向点B运动,当到达点B后继续沿BA向点A运动,速度是3cm/s,P,Q两点同时出发,从两点出发时开始计时,设运动的时间是t(s).
如图,在长方形ABCD中,AD=BC=12cm,AB=DC=8cm,动点P从点A出发沿AD向点D运动,速度是1cm/s,动点Q从点C出发沿CB向点B运动,当到达点B后继续沿BA向点A运动,速度是3cm/s,P,Q两点同时出发,从两点出发时开始计时,设运动的时间是t(s).(1)当点Q在线段BA上运动时,当t为何值时AP=AQ?
(2)当点Q在线段BC上运动时,t为何值时四边形PQCD的面积是长方形ABCD面积的
| 2 |
| 3 |
考点:一元一次方程的应用
专题:几何动点问题
分析:(1)根据等量关系:AP=AQ列出方程求解即可;
(2)根据等量关系:四边形PQCD的面积是长方形ABCD面积的
,由梯形和长方形的面积公式列出方程求解即可.
(2)根据等量关系:四边形PQCD的面积是长方形ABCD面积的
| 2 |
| 3 |
解答:解:(1)依题意有
t=12+8-3t,
解得t=5.
故当t为5s时AP=AQ;
(2)依题意有
×8(3t+12-t)=
×12×8,
解得t=2.
故当t为2s时四边形PQCD的面积是长方形ABCD面积的
.
t=12+8-3t,
解得t=5.
故当t为5s时AP=AQ;
(2)依题意有
| 1 |
| 2 |
| 2 |
| 3 |
解得t=2.
故当t为2s时四边形PQCD的面积是长方形ABCD面积的
| 2 |
| 3 |
点评:考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
己知某企业第一季度盈利26000元,第二季度亏本3000元,该企业上半年盈利(或亏本)可用算式表示为( )
| A、(+26000)+(+3000) |
| B、(-26000)+(3000) |
| C、(-26000)+(-3000) |
| D、(+26000)+(-3000) |
如果存入500元记为+500元,那么支出300元记为( )
| A、+300元 |
| B、-300元 |
| C、+200元 |
| D、-200元 |
