题目内容
如图,已知∠OA1A2=∠OA2A3=∠OA3A4=∠OA4A5=…=90°,且OA1=A1A2=A2A3=A3A4=A4A5=…=1,S1表示△OA1A2的面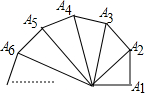 积,S2表示△OA2A3的面积,…,
积,S2表示△OA2A3的面积,…,细心观察图形,解答下列问题:
(1)0A2=
(2)请用含有n(n是正整数)的等式表示:OAn=
(3)求出S12+S22+S32+…S102的值.
分析:此题为勾股定理的运用,但分析可知,其内部存在一定的规律性,找出其内在规律即可解题,因为∠OA1A2=∠OA2A3=∠OA3A4=∠OA4A5=…=90°,且OA1=A1A2=A2A3=A3A4=A4A5=…=1,
即每个三角形最外的那条直角边均为1,则由图可得出OAn=
,Sn=
,
分析到此,即可解题.
即每个三角形最外的那条直角边均为1,则由图可得出OAn=
| n |
| ||
| 2 |
分析到此,即可解题.
解答:解:(1)
;
;
;
;各(1分),共(4分)
(2)由题意可知,OA1=
,OA2=
,OA3=
,…,所以OAn=
;(2分)
(3)原式=
=
.(2分)
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
(2)由题意可知,OA1=
| 1 |
| 2 |
| 3 |
| n |
(3)原式=
| 1+2+3+4+5+6+7+8+9+10 |
| 4 |
| 55 |
| 4 |
点评:此题主要考查的是勾股定理的运用以及规律的探查.

练习册系列答案
相关题目
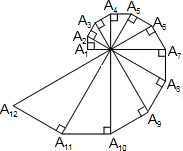 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2010OA2011的最小边长为( )
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2010OA2011的最小边长为( )| A、22009 | ||||
| B、22010 | ||||
C、(
| ||||
D、(
|
 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则A2A3=
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则A2A3= 积,S2表示△OA2A3的面积,…,
积,S2表示△OA2A3的面积,…,