题目内容
正方形ABCD的四个顶点都在⊙O上,E是⊙O上的一点.(1)如图①,若点E在
 上,F是DE上的一点,DF=BE.求证:△ADF≌△ABE;
上,F是DE上的一点,DF=BE.求证:△ADF≌△ABE;(2)在(1)的条件下,小明还发现线段DE、BE、AE之间满足等量关系:DE-BE=
 AE.请你说明理由;
AE.请你说明理由;(3)如图②,若点E在
 上.写出线段DE、BE、AE之间的等量关系.(不必证明)
上.写出线段DE、BE、AE之间的等量关系.(不必证明)
【答案】分析:(1)中易证AD=AB,EB=DF,所以只需证明∠ADF=∠ABE,利用同弧所对的圆周角相等不难得出,从而证明全等;
(2)中易证△AEF是等腰直角三角形,所以EF= AE,所以只需证明DE-BE=EF即可,由BE=DF不难证明此问题;
AE,所以只需证明DE-BE=EF即可,由BE=DF不难证明此问题;
(3)类比(2)不难得出(3)的结论.
解答: 解:(1)在正方形ABCD中,AB=AD(1分)
解:(1)在正方形ABCD中,AB=AD(1分)
∵∠1和∠2都对 ,
,
∴∠1=∠2,(3分)
在△ADF和△ABE中,
 ,
,
∴△ADF≌△ABE(SAS);(4分)
(2)由(1)有△ADF≌△ABE,
∴AF=AE,∠3=∠4.(5分)
在正方形ABCD中,∠BAD=90°.
∴∠BAF+∠3=90°.
∴∠BAF+∠4=90°.
∴∠EAF=90°.(6分)
∴△EAF是等腰直角三角形.
∴EF2=AE2+AF2.
∴EF2=2AE2.(7分)
∴EF= AE.(8分)
AE.(8分)
即DE-DF= AE.
AE.
∴DE-BE= AE.(9分)
AE.(9分)
(3)BE-DE= AE.理由如下:(12分)
AE.理由如下:(12分)
在BE上取点F,使BF=DE,连接AF.
易证△ADE≌△ABF,
∴AF=AE,∠DAE=∠BAF.(5分)
在正方形ABCD中,∠BAD=90°.
∴∠BAF+∠DAF=90°.
∴∠DAE+∠DAF=90°.
∴∠EAF=90°.(6分)
∴△EAF是等腰直角三角形.
∴EF2=AE2+AF2.
∴EF2=2AE2.(7分)
∴EF= AE.(8分)
AE.(8分)
即BE-BF= AE.
AE.
∴BE-DE= AE.(9分)
AE.(9分)
点评:本题主要考查圆周角定理,全等三角形的判定及勾股定理,难度适中.
(2)中易证△AEF是等腰直角三角形,所以EF=
 AE,所以只需证明DE-BE=EF即可,由BE=DF不难证明此问题;
AE,所以只需证明DE-BE=EF即可,由BE=DF不难证明此问题;(3)类比(2)不难得出(3)的结论.
解答:
 解:(1)在正方形ABCD中,AB=AD(1分)
解:(1)在正方形ABCD中,AB=AD(1分)∵∠1和∠2都对
 ,
,∴∠1=∠2,(3分)
在△ADF和△ABE中,
 ,
,∴△ADF≌△ABE(SAS);(4分)
(2)由(1)有△ADF≌△ABE,
∴AF=AE,∠3=∠4.(5分)
在正方形ABCD中,∠BAD=90°.
∴∠BAF+∠3=90°.
∴∠BAF+∠4=90°.
∴∠EAF=90°.(6分)
∴△EAF是等腰直角三角形.
∴EF2=AE2+AF2.
∴EF2=2AE2.(7分)
∴EF=
 AE.(8分)
AE.(8分)即DE-DF=
 AE.
AE.∴DE-BE=
 AE.(9分)
AE.(9分)(3)BE-DE=
 AE.理由如下:(12分)
AE.理由如下:(12分)
在BE上取点F,使BF=DE,连接AF.
易证△ADE≌△ABF,
∴AF=AE,∠DAE=∠BAF.(5分)
在正方形ABCD中,∠BAD=90°.
∴∠BAF+∠DAF=90°.
∴∠DAE+∠DAF=90°.
∴∠EAF=90°.(6分)
∴△EAF是等腰直角三角形.
∴EF2=AE2+AF2.
∴EF2=2AE2.(7分)
∴EF=
 AE.(8分)
AE.(8分)即BE-BF=
 AE.
AE.∴BE-DE=
 AE.(9分)
AE.(9分)点评:本题主要考查圆周角定理,全等三角形的判定及勾股定理,难度适中.

练习册系列答案
相关题目
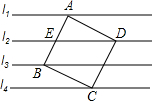 如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于h,若正方形ABCD的四个顶点分别在四条直线上,则它的面积等于( )
如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于h,若正方形ABCD的四个顶点分别在四条直线上,则它的面积等于( )| A、4h2 | ||
| B、5h2 | ||
C、4
| ||
D、5
|
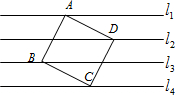 如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于1,若正方形ABCD的四个顶点分别在四条直线上,则它的面积等于( )
如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于1,若正方形ABCD的四个顶点分别在四条直线上,则它的面积等于( )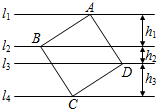 之间的距离依次为h1、h2、h3(h1>0,h2>0,h3>0).
之间的距离依次为h1、h2、h3(h1>0,h2>0,h3>0). 如图,已知⊙O中,直径MN=10,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45°,则AB的长为( )
如图,已知⊙O中,直径MN=10,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45°,则AB的长为( ) 如图,l1、l2、l3、l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h,面积是25的正方形ABCD的四个顶点分别在这四条直线上,那么h的值是
如图,l1、l2、l3、l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h,面积是25的正方形ABCD的四个顶点分别在这四条直线上,那么h的值是