题目内容
如图,港口B在港口A的西北方向,上午8时,一艘轮船从港口A出发,以15海里∕时的速度向正北方向航行,同时一艘快艇从港口B出发也向正北方向航行,上午10时轮船到达D处,同时快艇到达C处,测得C处在D处得北偏西30°的方向上,且C、D两地相距100海里,求快艇每小时航行多少海里?(结果精确到0.1海里∕时,参考数据 ≈1.41,
≈1.41, ≈1.73)
≈1.73)
解:过点C作AD的垂线,交AD的延长线于点F,过点A作CB的垂线,交CB的延长线于点E,

在直角三角形CDF中,∠CDF=30°,
∴CF= CD=50,
CD=50,
DF=CD•cos30°= ,
,
∵CF⊥AF,EA⊥AF,BE⊥AE,∴∠CEA=∠EAF=∠AFC=90°,
∴四边形AECF是矩形,
∴AE=CF=50,CE=AF,
在直角三角形AEB中,∠EAB=90°-45°=45°,
∴BE=AE=50,
∴CB=AD+DF-BE= ,
,
 (海里/时),
(海里/时),
答:快艇每小时航行33.3海里∕时.解析:
略

在直角三角形CDF中,∠CDF=30°,
∴CF=
 CD=50,
CD=50,DF=CD•cos30°=
 ,
,∵CF⊥AF,EA⊥AF,BE⊥AE,∴∠CEA=∠EAF=∠AFC=90°,
∴四边形AECF是矩形,
∴AE=CF=50,CE=AF,
在直角三角形AEB中,∠EAB=90°-45°=45°,
∴BE=AE=50,
∴CB=AD+DF-BE=
 ,
, (海里/时),
(海里/时),答:快艇每小时航行33.3海里∕时.解析:
略

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
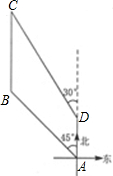 如图,港口B在港口A的西北方向,上午8时,一艘轮船从港口A出发,以15海里∕时的速度向正北方向航行,同时一艘快艇从港口B出发也向正北方向航行,上午10时轮船到达D处,同时快艇到达C处,测得C处在D处得北偏西30°的方向上,且C、D两地相距100海里,求快艇每小时航行多少海里?(结果精确到0.1海里∕时,参考数据
如图,港口B在港口A的西北方向,上午8时,一艘轮船从港口A出发,以15海里∕时的速度向正北方向航行,同时一艘快艇从港口B出发也向正北方向航行,上午10时轮船到达D处,同时快艇到达C处,测得C处在D处得北偏西30°的方向上,且C、D两地相距100海里,求快艇每小时航行多少海里?(结果精确到0.1海里∕时,参考数据 (2012•朝阳区二模)如图,港口B在港口A的东北方向,上午9时,一艘轮船从港口A出发,以16海里/时的速度向正东方向航行,同时一艘快艇从港口B出发也向正东方向航行.上午11时轮船到达C处,同时快艇到达D处,测得D处在C处的北偏东60°的方向上,且C、D两地相距80海里,求快艇每小时航行多少海里?(结果精确到0.1海里/时,参考数据:
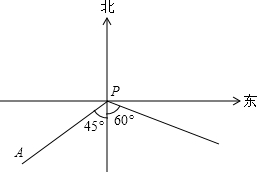
(2012•朝阳区二模)如图,港口B在港口A的东北方向,上午9时,一艘轮船从港口A出发,以16海里/时的速度向正东方向航行,同时一艘快艇从港口B出发也向正东方向航行.上午11时轮船到达C处,同时快艇到达D处,测得D处在C处的北偏东60°的方向上,且C、D两地相距80海里,求快艇每小时航行多少海里?(结果精确到0.1海里/时,参考数据: 如图,小岛A在港口P的南偏西45°方向,距离港口70海里处.甲船从A出发,沿AP方向以每小时20海里的速度驶向港口P;乙船从港口P出发,沿着南偏东60°方向,以每小时15海里的速度驶离港口.若两船同时出发.
如图,小岛A在港口P的南偏西45°方向,距离港口70海里处.甲船从A出发,沿AP方向以每小时20海里的速度驶向港口P;乙船从港口P出发,沿着南偏东60°方向,以每小时15海里的速度驶离港口.若两船同时出发.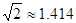 ,
, ,
, )
)
