Question

已知△ABC，以AC为边在△ABC外作等腰△ACD，其中AC=AD。
【小题1】如图1，以AB为边在△ABC外作等腰△ABE，其中AB=AE，，试证明BD=CE；
【小题2】如图2，若∠ABC=30°，△ACD是等边三角形，AB=3，BC=4，求BD的长；
【小题3】如图3，若∠ACB为锐角，作AH⊥BC于H，当BD²=4AH²+BC²时，问∠DAC与∠ABC有怎样的关系，直接写出结论（不需要证明）。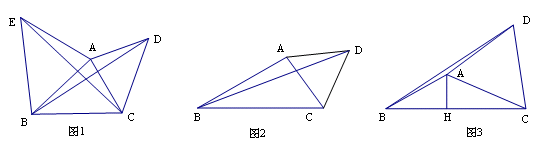

Answer 1

【小题1】∵∠BAE=∠CAD
∴∠CAE=∠BAD
∵AE=AB,AC=AD,
∴△ACE≌△ABD
∴BD=CE…….………………………………………………………………5分
【小题2】如图2，以A为顶点AB为边在外作=60°，并在AE上取AE=AB，连结BE和CE.                  ……………………………………7分

∵是等边三角形,
∴AD=AC，=60°.
∵=60°,
∴+=+.
即=.
∴≌.   ………………8分                                                                              
∴EC=BD.
∵=60°，AE=AB=3,
∴是等边三角形，
∴="60°," EB= 3， …………………9分
∵,
∴.
∵，EB=3，BC=4,
∴EC=5.
∴BD=5.             ……………………10分
【小题3】=2.       ……………………12分                              
附：证明：
如图３，过点B作BE∥AH，并在BE上取BE=2AH，连结EA，EC. 并取BE的中点K，连结AK.

∵于H，  ∴.  ∵BE∥AH,  ∴.
∵，BE=2AH,  ∴.
∵,  ∴EC=BD.
∵K为BE的中点，BE=2AH,  ∴BK=AH.
∵BK∥AH，  ∴四边形AKBH为平行四边形.
又∵,  ∴四边形AKBH为矩形.  ∴.
∴AK是BE的垂直平分线.  ∴AB=AE.
∵AB=AE，EC=BD，AC=AD,  ∴≌.                       
∴.  ∴.
即.  ∵，为锐角,  ∴.
∵AB=AE,  ∴.  ∴.  ∴=2.
∴=2  

解析