题目内容
已知△ABC的周长是50cm，中位线DE=8cm，EF=10cm，则另一条中位线DF=________．
7cm
分析：因为三角形的中位线等于第三边的一半，所以三条中位线的长为：50÷2=25，所求的中位线为25减去另两条中位线的长．
解答：∵△ABC的周长是50cm，
∴该三角形的三条中位线所组成的三角形的周长为50cm÷2=25cm，
∴另一条中位线DF的长为：25cm-8cm-10cm=7cm；
故答案是：7cm．
点评：本题考查了三角形中位线定理．解题时，利用了“三角形的中位线等于第三边的一半”求解．
分析：因为三角形的中位线等于第三边的一半，所以三条中位线的长为：50÷2=25，所求的中位线为25减去另两条中位线的长．
解答：∵△ABC的周长是50cm，
∴该三角形的三条中位线所组成的三角形的周长为50cm÷2=25cm，
∴另一条中位线DF的长为：25cm-8cm-10cm=7cm；
故答案是：7cm．
点评：本题考查了三角形中位线定理．解题时，利用了“三角形的中位线等于第三边的一半”求解．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
8、如图，已知△ABC的周长是34，其中AB=10，AO、BO分别是角平分线，且MN∥BA，分别交AC于N、BC于M，则△CMN的周长为（ ）已知△ABC的周长是24，且AB=AC，又AD⊥BC，D为垂足，若△ABD的周长是20，则AD的长为（ ）
| A、6 | B、8 | C、10 | D、12 |
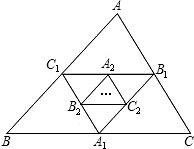如图：A1，B1，C1分别是BC，AC，AB的中点，A2，B2，C2分别是B1C1，A1C1，A1B1的中点…这样延续下去．已知△ABC的周长是1，△A1B1C1的周长是L1，△A2B2C2的周长是L2…AnBnCn的周长是Ln，则Ln=
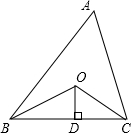如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，△ABC的面积是