题目内容
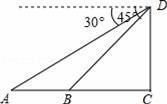
如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约是多少m?(精确到0.1m).(参考数据: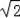
 ≈1.41,
≈1.41,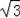
 ≈1.73)
≈1.73)

【考点】解直角三角形的应用-仰角俯角问题.
【分析】在Rt△ACD中,根据已知条件求出AC的值,再在Rt△BCD中,根据∠EDB=45°,求出BC=CD=21m,最后根据AB=AC﹣BC,代值计算即可.
【解答】解:∵在Rt△ACD中,CD=21m,∠DAC=30°,
∴AC=
 =
=
 =21
=21
 m,
m,
在Rt△BCD中,
∵∠EDB=45°,
∴∠DBC=45°,
∴BC=CD=21m,
∴AB=AC﹣BC=21
 ﹣21≈15.3(m);
﹣21≈15.3(m);
则河的宽度AB约是15.3m.


【点评】此题考查了解直角三角形的应用,用到的知识点是俯角、特殊角的三角函数值等知识点,关键是要求学生能借助俯角构造直角三角形并解直角三角形.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
| x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.
A.1 B.2 C.3 D.4


 在同一坐标系数中的大致图象是( )
在同一坐标系数中的大致图象是( )
 B.
B.
 C.
C.



 ,求⊙O的半径r.
,求⊙O的半径r.