题目内容
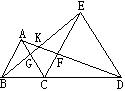
如图，C是线段BD上一点，分别以BC、CD为边长的BD同侧作等边三角形BCA和等边三角形CDE，连接BE、AD，分别交AC于M，交CE于N，若CM=x，则CN=________．
x
分析：易证△BCE≌△ACD，可得∠BEC=∠ADC，进而可求证△MCE≌△NCD，进而得CN=CM即可解题．
解答：在△BCE和△ACD中，
，
∴△BCE≌△ACD（SAS），
故∠BEC=∠ADC，
又CE=CD，∠MCN=∠NCD=60°，
∴△MCE≌△NCD（ASA），
∴CN=CM=x．
故答案为 x．
点评：本题考查了全等三角形的证明，全等三角形对应角、对应边相等的性质，等边三角形各内角为60°的性质，本题中求证△MCE≌△NCD是解题的关键．
分析：易证△BCE≌△ACD，可得∠BEC=∠ADC，进而可求证△MCE≌△NCD，进而得CN=CM即可解题．
解答：在△BCE和△ACD中，
，∴△BCE≌△ACD（SAS），
故∠BEC=∠ADC，
又CE=CD，∠MCN=∠NCD=60°，
∴△MCE≌△NCD（ASA），
∴CN=CM=x．
故答案为 x．
点评：本题考查了全等三角形的证明，全等三角形对应角、对应边相等的性质，等边三角形各内角为60°的性质，本题中求证△MCE≌△NCD是解题的关键．
练习册系列答案
相关题目
3、如图，C是线段BD上一点，分别以BC，CD为边在BD同侧作等边△ABC和等边△CDE，AD交CE于F，BE交AC于G，则图中可通过旋转而相互得到的全等三角形对数有（ ）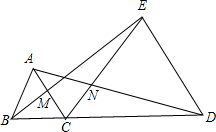
如图，C是线段BD上一点，分别以BC、CD为边长的BD同侧作等边三角形BCA和等边三角形CDE，连接BE、AD，分别交AC于M，交CE于N，若CM=x，则CN=
如图，C是线段BD上一点，分别以BC、CD为边作等边三角形ABC和CDE，连接AD、BE．求证：AD=BE．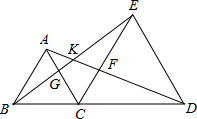
如图，C是线段BD上一点，分别以BC，CD为边在BD同侧作等边△ABC和等边△CDE，AD交CE于点F，BE交AC于点G，则图中可通过旋转而相互得到的三角形是：