题目内容
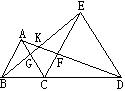
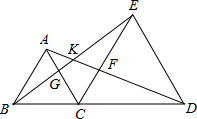 如图,C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于点F,BE交AC于点G,则图中可通过旋转而相互得到的三角形是:
如图,C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于点F,BE交AC于点G,则图中可通过旋转而相互得到的三角形是:△ACD绕点C逆时针旋转60°可得到△BCE;△FCD绕点C逆时针旋转60°可得到△GCE;
△ACD绕点C逆时针旋转60°可得到△BCE;△FCD绕点C逆时针旋转60°可得到△GCE;
(要求把符合条件的都写出来).分析:根据等边三角形的性质得到CA=CB,CD=CF,∠ACB=∠ECD=60°,根据旋转的定义即可得到△ACD绕点C逆时针旋转60°可得到△BCE;根据旋转的性质得∠BEC=∠ADC,又由于CE=CD,∠
GCE=∠FCD=60°,根据全等三角形的判定得到△FCD≌△GCE,则△FCD绕点C逆时针旋转60°可得到△GCE.
GCE=∠FCD=60°,根据全等三角形的判定得到△FCD≌△GCE,则△FCD绕点C逆时针旋转60°可得到△GCE.
解答:解:(1)∵△ABC和△CDE都是等边三角形,
∴CA=CB,CD=CF,∠ACB=∠ECD=60°,
∴△ACD绕点C逆时针旋转60°可得到△BCE;
(2)∵∠ACB=∠ECD=60°,
∴∠ACF=180°-60°-60°=60°,
∵ACD绕点C逆时针旋转60°可得到△BCE;
∴∠BEC=∠ADC,
在△FCD和△GCE中,
∵
,
∴△FCD≌△GCE(ASA),
∴△FCD绕点C逆时针旋转60°可得到△GCE.
故答案为△ACD绕点C逆时针旋转60°可得到△BCE;△FCD绕点C逆时针旋转60°可得到△GCE.
∴CA=CB,CD=CF,∠ACB=∠ECD=60°,
∴△ACD绕点C逆时针旋转60°可得到△BCE;
(2)∵∠ACB=∠ECD=60°,
∴∠ACF=180°-60°-60°=60°,
∵ACD绕点C逆时针旋转60°可得到△BCE;
∴∠BEC=∠ADC,
在△FCD和△GCE中,
∵
|
∴△FCD≌△GCE(ASA),
∴△FCD绕点C逆时针旋转60°可得到△GCE.
故答案为△ACD绕点C逆时针旋转60°可得到△BCE;△FCD绕点C逆时针旋转60°可得到△GCE.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目
 3、如图,C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的全等三角形对数有( )
3、如图,C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的全等三角形对数有( )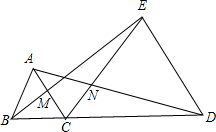 如图,C是线段BD上一点,分别以BC、CD为边长的BD同侧作等边三角形BCA和等边三角形CDE,连接BE、AD,分别交AC于M,交CE于N,若CM=x,则CN=
如图,C是线段BD上一点,分别以BC、CD为边长的BD同侧作等边三角形BCA和等边三角形CDE,连接BE、AD,分别交AC于M,交CE于N,若CM=x,则CN= 如图,C是线段BD上一点,分别以BC、CD为边作等边三角形ABC和CDE,连接AD、BE.求证:AD=BE.
如图,C是线段BD上一点,分别以BC、CD为边作等边三角形ABC和CDE,连接AD、BE.求证:AD=BE.