题目内容
在直角坐标系内，点P（-2，2
）到原点的距离为
| 6 |
2
| 7 |
2
．| 7 |
分析：在平面直角坐标系中描出P点，连接OP，过P作PQ垂直于x轴，由P的坐标得出PQ与OQ的长，在直角三角形OPQ中，由PQ与OQ的长，利用勾股定理求出OP的长，即为P到原点的距离．
解答：
解：连接OP，过P作PQ⊥x轴，交x轴于点Q，如图所示，
∵P（-2，2
），
∴PQ=2
，OQ=2，
在Rt△OPQ中，根据勾股定理得：OP=
=2
，
则P到原点的距离为2
．
故答案为：2
．
解：连接OP，过P作PQ⊥x轴，交x轴于点Q，如图所示，∵P（-2，2
| 6 |
∴PQ=2
| 6 |
在Rt△OPQ中，根据勾股定理得：OP=
| PQ2+OQ2 |
| 7 |
则P到原点的距离为2
| 7 |
故答案为：2
| 7 |
点评：此题考查了勾股定理，以及坐标与图形性质，熟练掌握勾股定理是解本题的关键．
练习册系列答案
相关题目
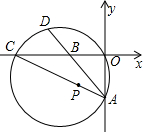AB的延长线交于点D，弧CD=弧AO，如果AB=10，AO＞BO，且AO、BO是x的二次方程x2+kx+48=0的两个根．