Question

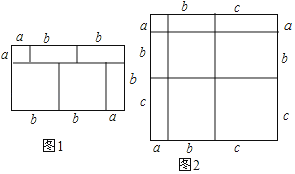
【题目】如图

（1）若∠2=∠3，则 ∥ ，理由是 ．

（2）若∠3=∠4，则 ∥ ，理由是 ．

（3）若m∥n，则∠1与∠4的关系是 ，理由是 ．

（4）若∠1+∠2=180°，则 ∥ ，理由是 ．

Answer 1

【答案】m;n; 同位角相等，两直线平行；a;b; 内错角相等，两直线平行；∠1+∠4=180°；两直线平行，同旁内角互补；a;b; 同旁内角互补, 两直线平行．

【解析】

（1）根据平行线的判定定理即可求解；

（2）根据平行线的判定定理即可求解；

（3）根据平行线的性质定理即可求解；

（4）根据平行线的判定定理即可求解．

（1）若∠2=∠3，则m∥n，理由是同位角相等，两直线平行．

（2）若∠3=∠4，则a∥b，理由是内错角相等，两直线平行．

（3）若m∥n，则∠1与∠4的关系是∠1+∠4=180°，理由是两直线平行，同旁内角互补．

（4）若∠1+∠2=180°，则a∥b，理由是同旁内角互补, 两直线平行．

故答案为：m;n; 同位角相等，两直线平行；a;b; 内错角相等，两直线平行；∠1+∠4=180°；两直线平行，同旁内角互补；a;b; 同旁内角互补, 两直线平行．