题目内容
16.设k为常数,已知直线l:y=kx-k+2,过点P(-1,0)作直线l的垂线,垂足为H,点A(3,-3),连接AH,则AH长度的最大值为5+$\sqrt{2}$.分析 由y=kx-k+2=(x-1)k+2可知直线过定点Q(1,2),根据题意垂足H在以直径PQ为直径的圆上,圆心为PQ的中点C(0,1),AH长度的最大值为AC+r.
解答 解:由y=kx-k+2=(x-1)k+2可知直线过定点Q(1,2),
∴垂足H在以直径PQ为直径的圆上,圆心为PQ的中点C(0,1),
∴其圆的方程为x2+(y-1)2=2,
|PC|=$\sqrt{{3}^{2}+(-3-1)^{2}}$=5,
∴AH长度的最大值为5+$\sqrt{2}$,
故答案为5+$\sqrt{2}$.
点评 本题考查了两条直线相交问题,二次函数的最值,求得圆心的坐标是解题的关键.

练习册系列答案
相关题目
7.如图,已知AB∥CD,∠1=60°,则∠2=( )


| A. | 60° | B. | 100° | C. | 120° | D. | 130° |
11.若关于x的二次三项式x2-ax+36是一个完全平方式,那么a的值是( )
| A. | 12 | B. | ±12 | C. | 6 | D. | ±6 |
 如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH为矩形,∠ADC+∠BCD应为90度.
如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH为矩形,∠ADC+∠BCD应为90度.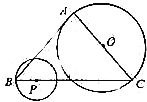 如图,在△ABC中,AB=AC=10,BC=12,点P为BC边上一动点,如果以P为圆心,BP为半径的圆P与以AC为直径的圆O相交,那么点P离开点B的距离BP的取值范围是$\frac{18}{7}$<BP<9.
如图,在△ABC中,AB=AC=10,BC=12,点P为BC边上一动点,如果以P为圆心,BP为半径的圆P与以AC为直径的圆O相交,那么点P离开点B的距离BP的取值范围是$\frac{18}{7}$<BP<9.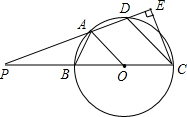 已知四边形ABCD内接于以BC为直径的⊙O,A为弧BD中点,延长CB,DA交于点P.
已知四边形ABCD内接于以BC为直径的⊙O,A为弧BD中点,延长CB,DA交于点P.