题目内容
1．若$\sqrt{5}$=a，$\sqrt{17}$=b，则$\sqrt{0.85}$的值使用a、b可以表示为$\frac{ab}{10}$．分析 $\sqrt{0.85}$=$\sqrt{\frac{85}{100}}$，再利用二次根式的乘除法法则化简即可．
解答 解：∵$\sqrt{5}$=a，$\sqrt{17}$=b，
∴$\sqrt{0.85}$=$\sqrt{\frac{85}{100}}$=$\frac{\sqrt{85}}{\sqrt{100}}$=$\frac{\sqrt{5}×\sqrt{17}}{10}$=$\frac{ab}{10}$．
故答案为$\frac{ab}{10}$．
点评 此题考查了算术平方根，二次根式的乘除法，解题的关键是把$\sqrt{0.85}$写成$\sqrt{\frac{85}{100}}$的形式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．
如图，在?ABCD中，AB=3，BC=5，∠ABC的平分线交AD于点E，则DE的长为（ ）
如图，在?ABCD中，AB=3，BC=5，∠ABC的平分线交AD于点E，则DE的长为（ ）| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
如图，在Rt△ABC中，BD是斜边AC上的中线，若AC=8，则BD的长=4．
6．在平面直角坐标系中，在第四象限内有一点P，且点P到x轴的距离是4，到y轴的距离是5，则点P的坐标为（ ）
| A． | （4，-5） | B． | （4，5） | C． | （-5，-4） | D． | （5，-4） |
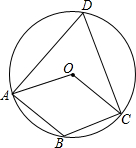如图，点A，B，C，D在⊙O上，点O在∠D的内部，四边形OABC为平行四边形，则∠OAD+∠OCD=60°．