题目内容
已知D、C为AE上的点，AD=CE，∠A=∠E，BC∥FD．求证：AB=EF．
证明：∵AD=CE，
∴AD+DC=CE+DC即AC=ED．
∵BC∥FD，
∴∠ACB=∠EDF．
在△ABC和△EFD中，
∵
，
∴△ABC≌△EFD（ASA）．
∴AB=EF．
分析：由已知条件先根据ASA判定△ABC≌△EFD，从而由三角形全等的性质求得AB=EF．
点评：主要考查全等三角形的判定，常用的判定方法有AAS，SSS，SAS，HL等．由平行线得到角相等是正确解答本题的关键．
∴AD+DC=CE+DC即AC=ED．
∵BC∥FD，
∴∠ACB=∠EDF．
在△ABC和△EFD中，
∵
，∴△ABC≌△EFD（ASA）．
∴AB=EF．
分析：由已知条件先根据ASA判定△ABC≌△EFD，从而由三角形全等的性质求得AB=EF．
点评：主要考查全等三角形的判定，常用的判定方法有AAS，SSS，SAS，HL等．由平行线得到角相等是正确解答本题的关键．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
如图，已知E、F分别为矩形ABCD的边BA、DC的延长线上的点，且AE=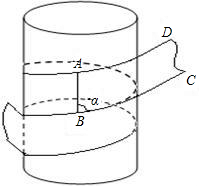
（任选一题做）
23、已知D、C为AE上的点，AD=CE，∠A=∠E，BC∥FD．求证：AB=EF．
（1）小明在一次实践活动课中，要对水管的外部进行包扎，包扎时用带子缠绕在管道外部．若要使带子全部包住管道且不重叠（不考虑管道两端的情况），需计算带子的缠绕角度α（α指缠绕中将部分带子拉成图中所示的平面ABCD时的∠ABC，其中AB为管道侧面母线的一部分）．若带子宽度为1，水管直径为2，则α的余弦值为______．
，AC上有一点E，满足AE：CE=2：3，则tan∠ADE的值是______．