题目内容
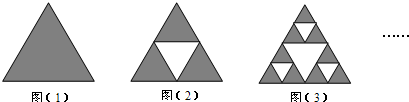
图（1）是一个面积为1的黑色正三角形，顺次连接它的三边的中点，得到如图（2）所示的第2个图形（它的中间为一个白色的正三角形）；在图（2）的每个黑色的正三角形中分别重复上述的作法，得到如图（3）所示的第3个图形．如此继续作下去，则在得到的第5个图形中，所有黑色三角形的面积和是 ．
【答案】分析：首先将所给的图②与图③中的黑色三角形的面积和求出来，注意利用相似三角形的面积比等于相似比的平方．然后得到规律：第n个图形中所有黑色三角形的面积和是：（
）n-1，代入即可求得．
解答：
解：∵D、E、F分别是AB、BC、CA的中点，
∴
，
∴△DEF∽△ABC，
∴
=（
）2=（
）2，
∴S△DEF=
，
∴图②中所有黑色三角形的面积和是：1-
=
，
同理：图三中各黑色三角形的面积和为：1-
×3-
=
=（
）2，
∴可得第n个图形中所有黑色三角形的面积和是：（
）n-1．
∴在得到的第5个图形中，所有黑色三角形的面积和是：（
）4．
故答案为：（
）4．
点评：此题考查了相似三角形的面积比等于相似比的平方．此题还考查了学生的分归纳能力．解题时要注意仔细分析．
）n-1，代入即可求得．解答：
解：∵D、E、F分别是AB、BC、CA的中点，
∴
，∴△DEF∽△ABC，
∴
=（）2=（）2，∴S△DEF=
，∴图②中所有黑色三角形的面积和是：1-
=，同理：图三中各黑色三角形的面积和为：1-
×3-==（）2，∴可得第n个图形中所有黑色三角形的面积和是：（
）n-1．∴在得到的第5个图形中，所有黑色三角形的面积和是：（
）4．故答案为：（
）4．点评：此题考查了相似三角形的面积比等于相似比的平方．此题还考查了学生的分归纳能力．解题时要注意仔细分析．
练习册系列答案
名校课堂系列答案
相关题目
