题目内容
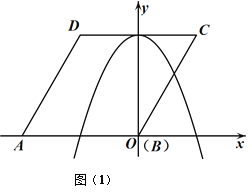
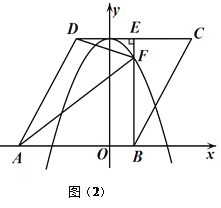
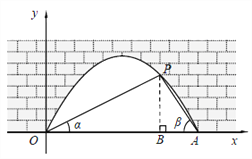
【题目】如图中是抛物线形拱桥，P处有一照明灯，水面OA宽4m，从O、A两处观测P处，仰角分别为α、β，且tanα=
，tanβ=
，以O为原点，OA所在直线为x轴建立直角坐标系.若水面上升1m，水面宽为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】分析：求出OB，PB的长得到点P的坐标，从而求出抛物线的解析式，再把y＝1代入抛物线的解析式中求横坐标，横坐标的差即是所要求的结果.
详解：设AB＝2b，则PB＝3b，OB＝6b，
所以OA＝8b，则8b＝4，所以b＝
，
所以OB＝
，PB＝
，则P(，
).
设抛物线的解析式为y＝ax(x－4)，
把x＝，y＝代入得
×(－4)a，解得x＝2±
，
所以水面上升1m后的宽为2＋－(2－)＝
.
故选A.
练习册系列答案
全能测控期末小状元系列答案
相关题目
