题目内容
如图,直线y=kx+2与x轴、y轴分别交于点A、B,点C(1,a)是直线与双曲线y=| m | x |
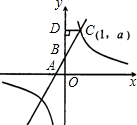 过点C作CD⊥y轴,垂足为D,且△BCD的面积为1.
过点C作CD⊥y轴,垂足为D,且△BCD的面积为1.(1)求双曲线的解析式;
(2)若在y轴上有一点E,使得以E、A、B为顶点的三角形与△BCD相似,求点E的坐标.
分析:(1)直线y=kx+2与y轴交于B点,则OB=2;由C(1,a)及△BCD的面积为1可得BD=2,所以a=4,即C(1,4),分别代入两个函数关系式中求解析式;
(2)根据△BAE∽△BCD、△BEA∽△BCD两种情形求解.
(2)根据△BAE∽△BCD、△BEA∽△BCD两种情形求解.
解答:解:(1)∵CD=1,△BCD的面积为1,
∴BD=2
∵直线y=kx+2与x轴、y轴分别交于点A、B,
∴当x=0时,y=2,
∴点B坐标为(0,2).
∴点D坐标为(O,4),
∴a=4.
∴C(1,4)
∴所求的双曲线解析式为y=
.
(2)因为直线y=kx+2过C点,
所以有4=k+2,k=2,
直线解析式为y=2x+2.
∴点A坐标为(-1,0),B(0,2),
∴AB=
,BC=
,
当△BAE∽△BCD时,此时点E与点O重合,点E坐标为(O,0);
当△BEA∽△BCD时,
=
,
∴
=
,
∴BE=
,
∴OE=
,
此时点E坐标为(0,-
).
综上:当E为(0.0)或(0.-
)时△EAB与△BCD相似.
∴BD=2
∵直线y=kx+2与x轴、y轴分别交于点A、B,
∴当x=0时,y=2,
∴点B坐标为(0,2).
∴点D坐标为(O,4),
∴a=4.
∴C(1,4)
∴所求的双曲线解析式为y=
| 4 |
| x |
(2)因为直线y=kx+2过C点,
所以有4=k+2,k=2,

直线解析式为y=2x+2.
∴点A坐标为(-1,0),B(0,2),
∴AB=
| 5 |
| 5 |
当△BAE∽△BCD时,此时点E与点O重合,点E坐标为(O,0);
当△BEA∽△BCD时,
| AB |
| DB |
| BE |
| BC |
∴
| ||
| 2 |
| BE | ||
|
∴BE=
| 5 |
| 2 |
∴OE=
| 1 |
| 2 |
此时点E坐标为(0,-
| 1 |
| 2 |
综上:当E为(0.0)或(0.-
| 1 |
| 2 |
点评:本题考查了反比例函数的综合应用,关键是求交点C的坐标以及相似形中的分类讨论思想,搞清楚对应关系.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
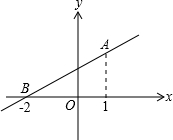 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为