题目内容
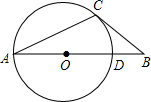（2012•三明）如图，在△ABC中，点O在AB上，以O为圆心的圆经过A，C两点，交AB于点D，已知∠A=α，∠B=β，且2α+β=90°．
（1）求证：BC是⊙O的切线；
（2）若OA=6，sinβ=
| 3 | 5 |
分析：（1）连接OC，则可得出∠A=∠ACO，从而利用外角的知识可得∠BOC=2α，再由2α+β=90°可判断出∠OCB=90°，继而可判断出BC是⊙O的切线．
（2）由（1）可得OC=OA=6，OC⊥BC，利用sinβ=
=
可求出OB的长度，在RT△OBC中利用勾股定理可得出BC的长度．
（2）由（1）可得OC=OA=6，OC⊥BC，利用sinβ=
| 3 |
| 5 |
| OC |
| OB |
解答：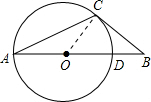
（1）证明：连接OC，
∵OA=OC，
∴∠ACO=∠A=α，
∵∠BOC=∠A+∠ACO=2α，
∴∠BOC+∠B=2α+β=90°，
∴∠BCO=90°，即OC⊥BC，
∵C在⊙O上，
∴BC是⊙O的切线．
（2）解：由（1）可得，OC=OA=6，OC⊥BC，
在Rt△BOC中，sinβ=
，
∵sinβ=
，
∴
=
，
∴OB=10，
∴BC=
=
=8．
（1）证明：连接OC，∵OA=OC，
∴∠ACO=∠A=α，
∵∠BOC=∠A+∠ACO=2α，
∴∠BOC+∠B=2α+β=90°，
∴∠BCO=90°，即OC⊥BC，
∵C在⊙O上，
∴BC是⊙O的切线．
（2）解：由（1）可得，OC=OA=6，OC⊥BC，
在Rt△BOC中，sinβ=
| OC |
| OB |
∵sinβ=
| 3 |
| 5 |
∴
| 3 |
| 5 |
| 6 |
| OB |
∴OB=10，
∴BC=
| OB2-OC2 |
| 102-62 |
点评：此题属于圆的综合题目，本题的第一问解法不止一种，同学们可以发散思维，多思考几种证明方法，在第二问的解答中，关键是利用sinβ的值求出OB的长度，有一定难度．
练习册系列答案
相关题目
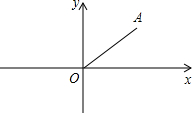（2012•三明）如图，在平面直角坐标系中，点A在第一象限，点P在x轴上，若以P，O，A为顶点的三角形是等腰三角形，则满足条件的点P共有（ ）
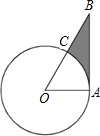（2012•三明）如图，AB是⊙O的切线，切点为A，OA=1，∠AOB=60°，则图中阴影部分的面积是（ ）
（2012•三明）如图是一个由相同小正方体搭成的几何体的俯视图，小正方形中的数字表示在该位置上的小正方体的个数，则这个几何体的左视图是（ ）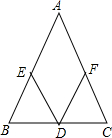
（2012•三明）如图，在△ABC中，D是BC边上的中点，∠BDE=∠CDF，请你添加一个条件，使DE=DF成立．你添加的条件是