题目内容
 在学习了全等三角形的判定方法后,刘老师给同学们出了如下的题目:“如图,点C、B在AD上,EA=FC,EA∥FC,请你补充一个条件,使△ABE≌△CDF”.小鹏回答:“∠E=∠F”,小彬回答:“EB=FD”,小莉回答:“AC=BD”,小华回答:“EB∥FD”.你认为他们四人说法正确的是
在学习了全等三角形的判定方法后,刘老师给同学们出了如下的题目:“如图,点C、B在AD上,EA=FC,EA∥FC,请你补充一个条件,使△ABE≌△CDF”.小鹏回答:“∠E=∠F”,小彬回答:“EB=FD”,小莉回答:“AC=BD”,小华回答:“EB∥FD”.你认为他们四人说法正确的是
- A.小鹏、小彬和小华
- B.小鹏、小莉和小华
- C.小鹏、小彬和小莉
- D.四人回答都正确
B
分析:根据全等三角形的判定定理,小鹏的符合ASA、小莉的符合SAS和小华的符合AAS,而小彬的是ASS,没有这个判定定理,从而得出小鹏、小莉和小华的说法正确.
解答:小鹏的说法符合ASA:
∵EA∥FC,∴∠A=∠DCF,
∵EA=FC,∠E=∠F,
∴△ABE≌△CDF;
小莉的说法符合SAS:
∵EA∥FC,∴∠A=∠DCF,
∵AC=BD,∴AB=CD,
∵EA=FC,
∴△ABE≌△CDF;
小华的说法符合AAS:
∵EA∥FC,∴∠A=∠DCF,
∵EB∥FD,∴∠ABE=∠CDF
∵EA=FC,
∴△ABE≌△CDF;
而小彬的说法不符合三角形全等的证明,
故说法正确的有小鹏、小莉和小华.
故选B.
点评:本题考查了全等三角形的判定,是基础知识要熟练掌握.
分析:根据全等三角形的判定定理,小鹏的符合ASA、小莉的符合SAS和小华的符合AAS,而小彬的是ASS,没有这个判定定理,从而得出小鹏、小莉和小华的说法正确.
解答:小鹏的说法符合ASA:
∵EA∥FC,∴∠A=∠DCF,
∵EA=FC,∠E=∠F,
∴△ABE≌△CDF;
小莉的说法符合SAS:
∵EA∥FC,∴∠A=∠DCF,
∵AC=BD,∴AB=CD,
∵EA=FC,
∴△ABE≌△CDF;
小华的说法符合AAS:
∵EA∥FC,∴∠A=∠DCF,
∵EB∥FD,∴∠ABE=∠CDF
∵EA=FC,
∴△ABE≌△CDF;
而小彬的说法不符合三角形全等的证明,
故说法正确的有小鹏、小莉和小华.
故选B.
点评:本题考查了全等三角形的判定,是基础知识要熟练掌握.

练习册系列答案
相关题目
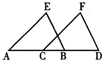 13、在学习了全等三角形的判定方法后,刘老师给同学们出了如下的题目:“如图,点C、B在AD上,
13、在学习了全等三角形的判定方法后,刘老师给同学们出了如下的题目:“如图,点C、B在AD上,
